Sin п/3 cos3x-cos п/3sin3x≥1
Другие вопросы по теме Алгебра
Популярные вопросы
- Розгляньте рисунок 2 і вкажіть пра />...
3 - Вычислить площадь фигуры, ограниченной линиями у = 2x + 4, у = 4 – х, у...
1 - 15.Переведите на английский язык. 1. Находишься ли ты в здании суда уже...
3 - 1. Какой характерной особенностью обладают диэлектрики? 2. Кислотное число...
3 - 0 E-01 - 6 - 25 Решите неравенство...
3 - (_1^2)Н+(_1^2)Н → (_2^4)Не термоядролық реакциясы кезінде қандай энергия...
1 - 1 Назовите виды основных погрешностей и как они определяются. 2 По каким...
2 - и Лучший ответ ФОРМУЛА ПОВНОЇ ЙМОВІРНОСТІ І ФОРМУЛА БАЙЄСА Задачі 3.13.1....
2 - Переведите с русского на английский используя ключевые фразы урока 1.( ключевые...
3 - Які особливості притаманні усній формі мовлення...
2
Объяснение:
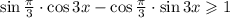
Заметим , что можно применить формулу
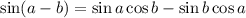

 находиться в промежутке
находиться в промежутке
 не может принимать значение меньшее -1 )
не может принимать значение меньшее -1 )
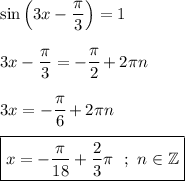
Тогда
Т.к область значения функции
y ∈ [ -1 ; 1 ]
То данное неравенство будет выполняться , только тогда когда
будет выполняться равенство
( т.к функция