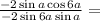Sin 5α − sin 7α / cos 7α − cos 5α = ctg 6α
Доказать тождество
Другие вопросы по теме Алгебра
Популярные вопросы
- Машина проехала 70 км. этот путь составил 2/5 части всего пути. определите сколько...
3 - Выполни деление с остатком и сделай проверку. 379: 12=? 680: 17=? 465: 32=? 803:...
3 - Преобразуйте простые предложения в ссп(сложноподчинённые) а/туристы преодолели...
1 - Игорь нарисовал прямоугольник со сторонами 6см. и 8см.четвёртую часть площади он...
3 - Диагонали ромба 4 см и 8 см верно ли что а) 32 см б) 16 см в) 12 см...
1 - Решить . на кухне в день дежурства не оказалось гирь для чашечных весов. нуж- но...
3 - Реши . школа заказала в швейную мастерскую форму для учащихся.одна швея может выполнить...
1 - Реакции в растворах электролита в не протекают до конца если а) выделяется газ...
2 - Нада 1) в середине века была распространена концепция четырех царств мира тюркские...
2 - Надеюсь на ! напишите программу которая задает массив из 15 элементов случайным...
1
Используем формулы разность синусов и разность косинусов:
sin(a) - sin(b) ≡ 2·sin( (a-b)/2 )·cos( (a+b)/2).
cos(a) - cos(b) ≡ -2·sin( (a+b)/2)·sin( (a-b)/2).
Тогда sin(5a) - sin(7a) ≡ 2·sin( (5a - 7a)/2)·cos( (5a+7a)/2) ≡
≡ 2·sin(-a)·cos(6a) ≡ -2·sin(a)·cos(6a).
cos(7a) - cos(5a) = -2sin( (7a+5a)/2)·sin( (7a - 5a)/2) ≡
≡ - 2sin(6a)·sin(a).
левая часть ≡