Середнє арифметичне двох чисел дорівнює 7, а різниця квадратів 14. знайти суму квадратів цих чисел
Другие вопросы по теме Алгебра
Популярные вопросы
- (4- y=2,x+2y=5. Решите как систему. Заранее...
1 - Екі өлеңді салыстыр.Өлең жолдарын тауып оқы даю ...
1 - Выдели подлежащее и сказуемое в словосочетаниях дедушка в деревне? мы в деревне...
1 - С развёртки постройте модель многогранника. Какой многогранник получится? Сколько...
1 - Градусні міри трьох внутрішніх кутів трикутника - це три послідовних парних числа....
3 - Сергей потратил в интернет-магазине 2003 руб. На покупку флеш-карты он израсходовал...
3 - Какие чувства воспитательного характера возникли после прочтения рассказа Кукла...
2 - Подготовить сообщение(рассмотреть лазерную обработку материалов,электронно-лучевую...
3 - Обчислити масу гідроксиду у розчині масою 200 г з масовою часткою 40 відсотків...
2 - Прочитайте утверждение. Приведите не менее 2 аргументов «за» и не менее 2 аргументов...
3
Нехай x та y - невідомі числа
За умовою задачі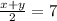 , а
, а 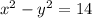
Якщо поділити вирази один на одний, отримуємо:
Тобто у нас виходить, що:
Отже одне число 6,5,а друге - 6,5+1=7,5
Составим систему
1 уравнение решаем
x+y=14
x= 14-y
Подставляем во второе
x= 14-6.5=7,5
ответ: 98,5
Чувак сверху не до конца решил