1. Алгебра
  2. с заданием! Вычислить несобственные

с заданием! Вычислить несобственные интегралы или установить их расходимость:


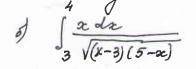
с заданием! Вычислить несобственные интегралы или установить их рас

микки37 микки37    2   16.06.2020 20:10    1

Ответы
SashaZaisnik1 SashaZaisnik1  15.10.2020 14:12

2\pi - 1

Объяснение:

Подыинтегральная функция на указанном промежутке интегрирования имеет единственную особенность в точке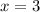 x=3. Исследовать интеграл на сходимость в этой точке можно с признака сравнения. В окрестности данной точки данный интеграл эквивалентен интегралу:

\int\limits_{3}^{4} \frac{dx}{\sqrt{x-3}} = 2\sqrt{x-3}|^{4}_{3} = 2,

то есть исходный интеграл сходится на заданном промежутке. Найдем его:

\int\limits_{3}^{4} \frac{x}{\sqrt{(x-3)(5-x)}}\,dx = \int\limits_{3}^{4} \frac{x}{\sqrt{-x^2+8x-15}}\,dx = -\frac{1}{2}\int\limits_{3}^{4} \frac{-2x+8-8}{\sqrt{-x^2+8x-15}}\,dx = -\frac{1}{2}\int\limits_{3}^{4} \frac{-2x+8}{\sqrt{-x^2+8x-15}}\,dx + \frac{1}{2}\int\limits_{3}^{4} \frac{8}{\sqrt{-x^2+8x-15}}\,dx = -\frac{1}{2}\int\limits_{3}^{4} \frac{d(-x^2+8x-15)}{\sqrt{-x^2+8x-15}}\,dx+ 4\int\limits_{3}^{4} \frac{d(x-4)}{\sqrt{1-(x-4)^2}} = -\sqrt{-x^2+8x-15}|^{4}_{3} + 4arcsin(x-4)|^{4}_{3} = -1+2\pi

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
1ЛиКа6 1ЛиКа6  21.07.2019 10:20
1) ctg 11π/6 2) cos 10π 3) sin 1110 4)ctg (-20π/3)...
Milena251267 Milena251267  21.07.2019 10:20
20 одна ! во сколько раз нужно уменьшить каждую сторону ромба чтобы получить ромб,подобный данному,с периметром n раз меньше периметра данного ромба....
lthyperdeath1 lthyperdeath1  21.07.2019 10:20
Представьте в виде произведения: (у-6)²-9у²=...
Cociheyuajnqhvedoxbs Cociheyuajnqhvedoxbs  21.07.2019 10:20
Решите, a)y=4x^2+4x-3 б)y=-3x^2-2x+1 в) y=-2x^2+3x+2...
Капуста11111 Капуста11111  21.07.2019 10:20
Уменя с ответом никак не сходится, sin(-11π/6)cos(-13π/6)tg(-5π/4)ctg(-5π/3) ответ должен быть -1/4, но как?...
Такблэт228 Такблэт228  21.07.2019 10:20
Разложите на множители: 1) (2а-3)^2-81, 2) (3b-4)^2 - (b+7)^2, 3) m^6 - (m^2 - 3)^2, 4) (a-b-c)^2 - (a+b-c)^2...
простой221 простой221  27.06.2019 07:10
Из системы уравнений xy=12.x+y=8.найти /х-у/,2,из системы уравнения x^2-3xy=6.x-3y=2 найти х...
1Kolomiets1 1Kolomiets1  27.06.2019 07:10
Нужно решить, ! 1. решить уравнение (3-2x)²=(2x-3)×(1-6x) ? 2. при каких значениях b уравнение 3x²+6x+1=0 - имеет корни? 3. вычислить координаты точек пересечения...
Аньсминожек Аньсминожек  27.06.2019 07:10
Решите хоть какое-то 1) sin(arccos √3/2) 2) tgx = -√3 3) 2sinx • cosx=0 4) 1-cos2x=2sinx 5) sin5x-sinx=0 6) cos5xcosx-sinxsin5x=0 7) cosx/1-sinx=0...
aika9626 aika9626  27.06.2019 07:10
Tga=4/15 вычеслить 5sina+7cosa/ 6cosa-3sina...

Популярные вопросы