Алгебра: с тригонометрией 3 примера

с тригонометрией 3 примера

Ответы

stefa4 26.11.2021 08:56

Не люблю задания, в которых больше одной задачи. Но эти задачи симпатичные, допускающие не совсем стандартные рассуждения. Вот ради этих рассуждений я и берусь за решение задач.

4.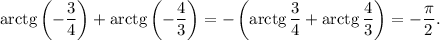 ${\rm arctg} \left(-\dfrac{3}{4}\right)+{\rm arctg} \left(-\dfrac{4}{3}\right)=-\left({\rm arctg}\, \dfrac{3}{4}+{\rm arctg \,\dfrac{4}{3}\right)=-\dfrac{\pi}{2}.$ ответ: - 1

Объяснение: арктангенс трех четвертых и арктангенс четырех третьих - это острые углы в прямоугольном треугольнике с катетами 3 и 4, поэтому их сумма равна 90 градусам.

6. арктангенсы одной второй и одной третьей меньше 45 градусов, поэтому их сумма лежит в первой четверти. Воспользуемся формулой

${\rm tg}(x+y)=\dfrac{{\rm tg}\, x+{\rm tg}\, y}{1-{\rm tg}\, x\cdot {\rm tg}\, y}.$

${\rm tg}\, ({\rm{arctg}\, \frac{1}{2}+{\rm{arctg}\, \frac{1}{3})=\dfrac{\frac{1}{2}+\frac{1}{3}}{1-\frac{1}{2}\cdot\frac{1}{3}}=1\Rightarrow {\rm arctg}\,\frac{1}{2}+{\rm arctg}\, \frac{1}{3}=\dfrac{\pi}{4}.$

Осталось сосчитать синус полученного угла и возвести результат в квадрат. ответ: 0,5

5. Арксинус 4/5 - это острый угол (лежащий против катета, равного 4) прямоугольного треугольника ABC с катетами BC=4 и AC=3 и гипотенузой AB=5. Нас интересует половина этого угла, поэтому рисуем биссектрису AD , которая поделит катет BC на отрезки CD=3/2 и DB=5/2, пропорциональные боковым сторонам. В прямоугольном треугольнике ADC катеты AC=3; CD=3/2. Чтобы упростить вычисления, рассмотрим подобный ему треугольник A'D'C' с катетами A'C'=2 и C'D'=1 и гипотенузой A'D'=корень из 5. Интересующий нас угол, равный половине арксинуса 4/5 - это угол A' этого треугольника, а второй острый угол равен арктангенсу 2. Поэтому

$\frac{1}{2}\arcsin \frac{4}{5}-2{\rm arctg}\, (-2)=\frac{1}{2}\arcsin\frac{4}{5}+2{\rm arctg}\, 2=\dfrac{\pi}{2}+{\rm arctg}\, 2;$