Розв'яжіть: 2sin x cos x = 2cos ( - ) -√3 = 0
Ответы
По формуле синуса двойного аргумента:
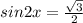
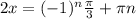 , n ∈ Z
, n ∈ Z
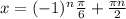 , n ∈ Z
, n ∈ Z
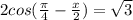
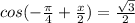
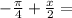 ±
±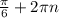 , n ∈ Z
, n ∈ Z
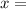 ±
±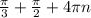 , n ∈ Z
, n ∈ Z
ПОКАЗАТЬ ОТВЕТЫ
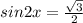
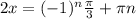 , n ∈ Z
, n ∈ Z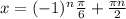 , n ∈ Z
, n ∈ Z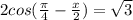
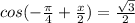
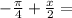 ±
±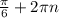 , n ∈ Z
, n ∈ Z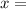 ±
±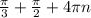 , n ∈ Z
, n ∈ Z
Другие вопросы по теме Алгебра
Популярные вопросы
- От скрещивания комолого быка айширской породы с рогатым коровами...
3 - Родители имеют I и II группы крови. Какие группы крови следует...
2 - Расскажите, как вы понимаете выражение «системный характер генотипа»....
3 - Почему триплоидные сорта некоторых видов растений считаются более...
2 - Нормальный слух у человека обусловлен доминантным геном S, а...
1 - У родителей со свободной мочкой уха и треугольной ямкой на подбородке...
3 - Черный цвет щетины у свиней доминирует над рыжим. Какое потомство...
3 - Как влияет на проявление признаков организма комплементарное...
1 - Женщина с карими глазами и рыжими волосами вышла замуж за мужчину...
2 - Черная окраска меха у норок доминирует над голубой. Как доказать...
1