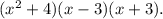Розкладіть на множники тричлен х^4-5х^2-36
Другие вопросы по теме Алгебра
Популярные вопросы
- Через вершину B тупого угла параллелограмма ABCD проведена прямая BM, перпендикулярная...
3 - Плоскость а проходит через вершину A треугольника ABC и параллельна прямой...
2 - ABCDA1B1C1D1 — прямоугольный параллелепипед (рис. 173, а). а) Верно ли, что...
1 - Через вершину A квадрата ABCD проведена прямая AO, перпендикулярная его плоскости....
3 - В треугольной пирамиде SABC боковое ребро SB перпендикулярно плоскости основания...
3 - Прямая OB перпендикулярна плоскости квадрата ABCD. Найдите площадь треугольника...
3 - Дан куб ABCDA1B1C1D1. Вычислите расстояние между прямыми B1D и D1C, если...
1 - Из точки A к плоскости а проведены перпендикуляр AB и наклонные AC и AD,...
1 - Прямая OS перпендикулярна плоскости ромба ABCD, диагонали которого пересекаются...
1 - Основание треугольной пирамиды SABC — равнобедренный треугольник ABC, а боковое...
1
x⁴ - 5x² - 36 | x² = y
y² - 5y - 36 = 0 D = b²-4ac = 25+144 = 169
y₁₂ = (-b±√D)/2a
y₁ = (5+13):2 = 9
y₂ = (5-13):2 = -4
y² - 5y - 36 = (y - 9)(y + 4)
x⁴ - 5x² - 36 = (x² - 9)(x² + 4) = (x - 3)(x + 3)(x² + 4)
Для того чтобы разложить на множители выражение вида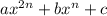 , где
, где 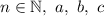 — числа, достаточно решить квадратное уравнение
— числа, достаточно решить квадратное уравнение 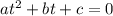 , где
, где 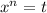 , и применить формулу разложения:
, и применить формулу разложения: 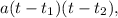 где
где 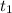 и
и 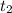 — корни данного квадратного уравнения, после чего нужно сделать обратную замену.
— корни данного квадратного уравнения, после чего нужно сделать обратную замену.
Итак, имеем биквадратный трехчлен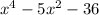 . Сделаем подходящую замену:
. Сделаем подходящую замену: 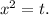 Получили квадратный трехчлен
Получили квадратный трехчлен 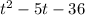 .
.
Решим уравнение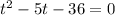 при теоремы Виета:
при теоремы Виета:
Получили корни: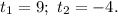
Подставим полученные корни в формулу: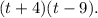 Сделаем обратную замену:
Сделаем обратную замену: 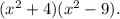 Применим формулу разности квадратов
Применим формулу разности квадратов 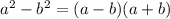 и получаем окончательное разложение данного биквадратного трехчлена:
и получаем окончательное разложение данного биквадратного трехчлена: 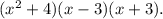
Воспользуемся методом группирования (группировки):
ответ: