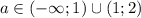Решите . Задание по алгебре.
Другие вопросы по теме Алгебра
Популярные вопросы
- Чему равна массовая доля железа в оксиде fe3o4...
1 - Сообщение о растениях растущих в сухих местах....
1 - Твір на тему як відображується козацтво у твору джури козака швайки (22 )...
2 - Ширину прямокутника зменшили на 50% . на скільки треба збільшити довжину прямокутника...
3 - Сочинение на тему тарас бульба - народный герой план 1 основа повести 2 тарас бульба...
2 - А.с.пушкин узник 1)какие средства художественной выразительности поэту передать...
3 - Напиште текст песни связанное с жизнью !...
3 - Определите, что будет выведено на экран после выполнения фрагмента программы на...
1 - Обеспечивает растение растение водой и другими полезными элементами,находящимся...
2 - Два поезда ехали с лдинаковой скоростью. первый был в дороге - 4 часа, второй -...
2
Объяснение:
Перенесём один из корней влево, а одну из семёрок — вправо следующим образом:
Рассмотрим функцию![f(x)=7^x+\sqrt[7]{x}](/tpl/images/4771/4253/5e929.png) . Она представляет собой сумму двух монотонно возрастающих функций (показательная и функция корня седьмой степени), следовательно она также монотонно возрастает. Значит, каждому аргументу соответствует ровно одно значение функции, то есть функция f(x) взаимно однозначна.
. Она представляет собой сумму двух монотонно возрастающих функций (показательная и функция корня седьмой степени), следовательно она также монотонно возрастает. Значит, каждому аргументу соответствует ровно одно значение функции, то есть функция f(x) взаимно однозначна.
Уравнение в таком случае принимает следующий вид:
Поскольку каждому значению функции соответствует только одно значение аргумента, равенство значений функции можно свести к равенству её аргументов:
Если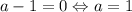 , то это линейное уравнение, имеющее не более одного корня, что не подходит.
, то это линейное уравнение, имеющее не более одного корня, что не подходит.
Если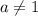 , то это квадратное уравнение. Оно имеет два корня при положительном дискриминанте:
, то это квадратное уравнение. Оно имеет два корня при положительном дискриминанте:
Учитывая, что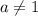 , получаем ответ
, получаем ответ