Решите уровнение 3sinx-4cosx f`(x)=0
Другие вопросы по теме Алгебра
Популярные вопросы
- Найдите сумму членов арифметической прогрессии -3.2; -2. не превосходящих...
3 - Это французский язык. переведите, , ! les chercheurs des universités de leicester...
1 - Эссе на тему: 《 сострадание в современном мире》...
3 - Решите неравенство 12х-8(х-3) 6-5х...
3 - Вставьте артикль там,где нужно: 1. these are mice. 2.he s got big teeth....
1 - :3 у чому полягає особливість поеми кавказ у наш час?...
2 - Встихе определить самостоятельные части речи.это сущ. прилог. местоим. числительное....
1 - Вставьте пропущенные буквы и обозначьте грамматические основы. составьте...
1 - Все что есть. знаю неплохо,но с составлением предложений у меня явные проблемы....
3 - Вкаком году появилась династия романовых...
1
Т.к. косинус и синус одновременно не могут быть равны нулю, поделим обе части уравнения на косинус не равный нулю.
ответ: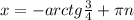 , n∈Z.
, n∈Z.