Решите уровнение
121а^3-16a=0
Другие вопросы по теме Алгебра
Популярные вопросы
- Зная солнечную постоянную для Земли, вычислите величину солнечной постоянной...
3 - Почему Юпитер иногда считают «несостоявшейся» звездой?...
2 - Проведите энергетический расчет термоядерной реакции синтеза ядер гелия-4...
2 - Почему при наблюдении с Земли вам кажется, что в течение ночи звезды...
3 - Почему иногда называют кометы «видимым ничто»? Как было доказано, что...
3 - Определите мощность излучения Солнца, если солнечная постоянная равна...
2 - Во сколько раз нужно было бы увеличить скорость вращения Земли вокруг...
3 - Опишите состав и возможное происхождение метеоритов....
2 - Зависит ли смена времен года от расстояния Земли от Солнца (в перигелии...
3 - Что характерно для осевого вращения спутников планет-гигантов вокруг...
2
Объяснение:
Вспомним формулу разности квадратов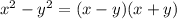 . В данном случае
. В данном случае 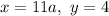
Произведение равно 0 тогда и только тогда, когда хотя бы один из множителей равен 0, а остальные при этом существуют