Решите уравнение с подробным объяснением.
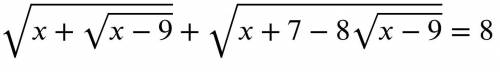
Другие вопросы по теме Алгебра
Популярные вопросы
- Если в ВУЗе дают только там , и то-что я сдавала ГТО, мне в ЕГЭ не начислят...
1 - Вычисли по действиям 2км308м*607-6км864м=???16кг560г:(20кг560г-19кг640г)=??...
1 - треугольник авс задан координатами своих вершин А(2;2;6) В(1;4;5) С(6;8;4)...
2 - 1. Заполните таблицу, внимательно изучив материал «История создания комедии»...
1 - Спишите предложения используя правильную форму прилагательного...
1 - Science fiction, thriller, autobiography, war story, horror story, spy story,...
1 - 5.Сізше, Қажымұраттың сауығуына мүмкіндігі бар ма? Жауабыңыздыдәлелмен келтіріңіз....
2 - Найти площадь треугольника со сторонами 8 дм, 29дм, 35 дм. ...
3 - Внешний угол треугольника равен 109°, а внутренний угол, не смежный с ним,...
2 - Зжелайте таблицу сравнение национальных костюмов ( головной убор, основной...
3
Объяснение:
Рассмотрим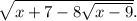
ответ: x=38,16.