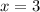Решите уравнение перейдя в логарифмах к известному основанию
Другие вопросы по теме Алгебра
Популярные вопросы
- Окаких обитателях моря рассказал писатель в.катаев? как звали героя повести...
1 - Рулон ткани, в котором пятьдесят погонных метров, стоит 4000 рублей....
2 - Какой можно придумать как можно , как часто делятся клетки одноклеточной...
1 - Окончание слова пробирается за верный ответ 25...
3 - Месяц назад 2 мороженых стоили 12 руб сейчас их цена увеличилась на 2...
3 - Успортивному залі лежить 6 сіток з великими мячами, по 3 мяча в кожній...
2 - Тело брошено под углом 60 degree к горизонту с горизонтальной поверхности...
1 - Мотоциклист проехал 180 км. какое расстояние может проехать за то же...
3 - Выпиши слова,в которых количество букв и звуков одинаковое.яма,жир,уголь,ручка....
3 - Начерти прямой угол с вершиной в точке о. отложи от точки о на сторонах...
2
Запишем ОДЗ: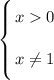
Воспользуемся свойством логарифма: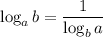
Итак, наше уравнение примет вид:
Сделаем замену: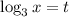
Имеем:
Обратная замена:
ответ: