Решите уравнение на фото.
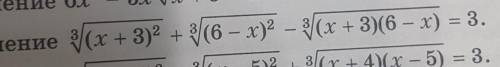
Другие вопросы по теме Алгебра
Популярные вопросы
- Compete the sentences below with the correct article if necessary is planet....
2 - Our tradiitional food is sausages.people have them for lunch and for dinner.i...
1 - Надо написать сочинение от древнего человека!...
3 - Образуй от данных слов слова с противоположным значением.выдели ту часть...
3 - Добавить 1 слог чтобы получилось слово...
1 - Из пункту а одновременно в противоположных направлениях выехали два автомобиля....
2 - Какой правильный ответ we will help you in an hour. или we help you in an...
2 - 3cos п/3 - 2 sin п/6 + 3tg п/4 - ctg п/4 думаю кто-нибудь...
3 - Вычисли периметр прямоугольника,длина которого 6 см,а ширина 3 см...
2 - Вычислите: 1)(4/5)2 /3)2 3)(1 1/2)2 1/4) 5)(2.1)2 )3 7)(9)3 )3 9)(1 3/4)3...
2
ответ: х₁=-2; х₂=5
Объяснение:
выражение в левой части равенства -это неполный квадрат))
можно домножить обе части равенства до суммы кубов...
обозначим: а=∛(х+3); b=∛(6-x); из уравнения очевидно, что a+b≠0
получим:
a² + b² - ab = 3
домножим обе части равенства на (a+b)≠0...
(a² - ab + b²)*(a+b) = 3(a+b)
a³ + b³ = 3(a+b)
вернемся к переменной (х):
х+3 + 6-х = 3(∛(х+3) + ∛(6-х))
9 = 3(∛(х+3) + ∛(6-х))
3 = ∛(х+3) + ∛(6-х)
или (в ранее введенных обозначениях)
3 = a+b
дальше можно по-разному... можно выразить: a=3-b
а можно вернуться к исходному уравнению и выделить полный квадрат (причем, квадрат суммы)))...
a² + b² - ab +2ab-2ab = 3
a² +2ab + b² -3ab = 3
(a+b)² = 3 + 3ab
(3)² = 3 + 3ab
9 = 3*(1+ab)
3 = 1 + ab
ab = 2
∛(х+3) * ∛(6-x) = 2
(x+3)*(6-x) = 8
6x - x² + 18 - 3x = 8
x² - 3x - 10 = 0 по т.Виета два корня... (5) и (-2)
Предположим, что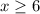 является корнем уравнения. Тогда последний корень неотрицателен. Стало быть, левая часть не меньше
является корнем уравнения. Тогда последний корень неотрицателен. Стало быть, левая часть не меньше ![\sqrt[3]{(6+3)^2} =3^{4/3}3](/tpl/images/1476/9468/2e007.png) , противоречие.
, противоречие.
Пусть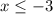 является корнем уравнения. Получаем аналогичную ситуацию.
является корнем уравнения. Получаем аналогичную ситуацию.
Значит, искомый корень лежит в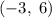 (*).
(*).
Пусть![\sqrt[3]{(x+3)^2}=a, \; \sqrt[3]{(6-x)^2} = b](/tpl/images/1476/9468/c8f10.png) . Тогда уравнение можно переписать в виде
. Тогда уравнение можно переписать в виде 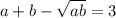 . Домножим обе части на
. Домножим обе части на 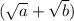 , получим:
, получим: 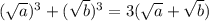 . Левая часть уравнения равна
. Левая часть уравнения равна 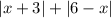 . С учетом (*) можно записать
. С учетом (*) можно записать 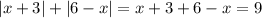 . Наконец,
. Наконец, 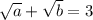 . Исходное уравнение:
. Исходное уравнение: 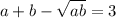 . Возводя в квадрат первое уравнение и складывая со вторым, умноженным на 2, получаем
. Возводя в квадрат первое уравнение и складывая со вторым, умноженным на 2, получаем 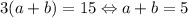 . Если теперь возведенное в квадрат первое уравнение вычесть из второго, получим
. Если теперь возведенное в квадрат первое уравнение вычесть из второго, получим 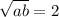 . Из этой системы следует два решения:
. Из этой системы следует два решения: 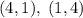 . Вернемся к исходному уравнению:
. Вернемся к исходному уравнению: 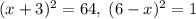 , откуда
, откуда 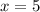 . Второй случай:
. Второй случай: 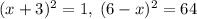 , откуда
, откуда  .
.