1. Алгебра
  2. Решите уравнение методом

Решите уравнение методом введения новой переменной: а)4x^{4}-17x^{2}+4=0 б)(x^{2}-2x)^{2}+(x^{2}-2x)=12

kartoshka212 kartoshka212    2   18.05.2019 19:10    18

Ответы
danilsalnikov danilsalnikov  12.06.2020 00:51

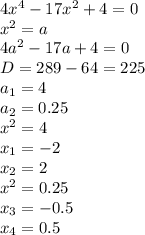
а)4x^{4}-17x^{2}+4=0\\x^2=a\\ 4a^2-17a+4=0\\ D=289-64=225\\a_1=4\\a_2=0.25\\ x^2=4\\x_1=-2\\x_2=2\\ x^2=0.25\\x_3=-0.5\\x_4=0.5

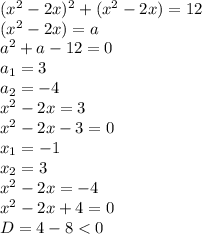
б)(x^{2}-2x)^{2}+(x^{2}-2x)=12\\ (x^{2}-2x)=a\\ a^2+a-12=0\\ a_1=3\\a_2=-4\\ x^2-2x=3\\x^2-2x-3=0\\x_1=-1\\x_2=3\\x^2-2x=-4\\x^2-2x+4=0\\D=4-8<0

корней нет

ответ: -1; 3

ПОКАЗАТЬ ОТВЕТЫ
lesbekdauren1 lesbekdauren1  12.06.2020 00:51

1) пусть х^2 = y

4у^2-17y+4=0

Д=289-64=225

у1=4

у2=0,25

следовательно

х=+- 0,5

х=+-2

2)пусть х^2-2x=y

 y^2+y-12=0

Д=1+48=49

y1=3

y2=-4

cледовательно

1)x^2-2x-3=0

Д=4+12=16

х1=3

х2=-1

2)x^2-2x+4=0

нет решений

 

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Натама Натама  18.01.2021 21:26
Всем привет решите дванеравенства...
vladaplakhotya vladaplakhotya  18.01.2021 21:25
Укажите на числовой окружности точку, которая соответствует числу: 1)- п/2 2)9п/4 3)- 10п/3 4) 32п/6 5)- 11/8 п 6)17п/4 (где минусы написаны с пробелом, они относятся ко всей дроби....
A01AA0 A01AA0  18.01.2021 21:25
Решите методом подстановки уравнений​...
gigi81 gigi81  18.01.2021 21:25
392 От станции до озера турист доехал на велосипеде за 2 ч. Пеш- ком он мог бы пройти это расстояние за 6 ч. Чему равно рас-стояние от станции до озера, если на велосипеде турист...
дима22819 дима22819  18.01.2021 21:23
Привет всем решить два неравенства...
Aliskaliska27 Aliskaliska27  18.01.2021 21:19
-1x^2+3=0 x^2+9x=0 Найти корни и D...
SamForDevil SamForDevil  18.01.2021 21:18
«Математическое ожидание и дисперсия и средне квадратичное отклонение случайной величины». Найти Р 2...
toktamuratovanilufar toktamuratovanilufar  28.05.2020 20:01
А здесь нужно решить одно задание на интегралы. Задание под номером 7.5. Задание звучит так: вычислить интегралы....
Plild Plild  27.05.2020 20:01
Які з функцій визначені на всій числовій осі: А) у = 2х- 1; Б) у = х2 +4; В) у = х-1 - 12; Г) у = √x+3. НА...
logan8 logan8  27.05.2020 20:01
Яка з нерівностей є хибною при всіх значеннях х? (х – 1)2 0 - х2 + 10 0 (х – 5)2 0 х2 + 10 0...

Популярные вопросы