Решите уравнение:
корень 1 - x - корень 13 + x = корень x + 4

Indira6767 3 26.12.2020 23:54 606

Question

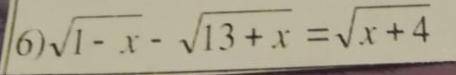
Алгебра: Решите уравнение: корень 1 - x - корень 13 + x = корень x + 4

Indira6767 · Answer

Таких Х (на вещественной оси) не существует или по простому Х∈∅

Объяснение:

ОДЗ:

Х∈[-13;1]

Перенесём -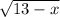 $\sqrt{13-x}$ направо и возведём обе части в квадрат.

получим:

$1-x=2x+17+2\sqrt{(x+4)(x+13)}$

Уединим корень и снова возведём в квадрат:

$(-16-3x)^{2}=(2\sqrt{(x+4)(x+13)})^{2} \\9x^{2} +96x+256=4(x^{2} +17x+52) \\5x^{2} +28x+48=0$

Посчитаем дискриминант:

D=28^2-4*48*5=-176

Т.к. он отрицательный Х, удовлетворяющих начальному уравнению, нет.

Решите уравнение: корень 1 - x - корень 13 + x = корень x + 4