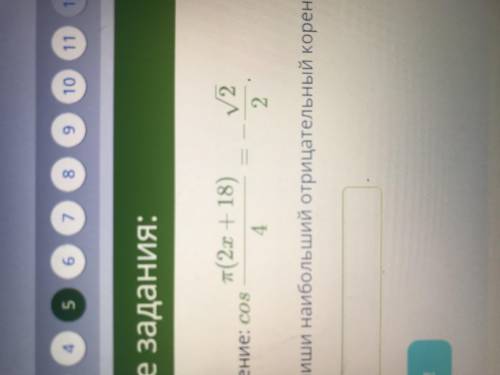
Решите уравнение

cos P(2x+18)/4=-2/2

в ответе записать наибольший отрицательный корень

Для решения данного уравнения, мы применим следующие шаги:

Шаг 1: Перепишем уравнение и приведем его к более простой форме:
cos(P(2x+18)/4) = -2/2
Мы заменим -2/2 на -1, так как они имеют одно и то же значение.

Шаг 2: Выразим аргумент косинуса, который находится внутри функции, в отдельную переменную:
Пусть Y = (2x + 18)/4
Тогда, уравнение будет выглядеть так:
cos(PY) = -1

Шаг 3: Используем график функции косинуса для определения значений угла, при которых cos(PY) = -1.
На графике функции косинуса, значения равные -1, достигаются при значениях угла (PY), равных π + 2πn, где n - любое целое число.
Таким образом, уравнение становится:
PY = π + 2πn

Шаг 4: Подставим обратно Y из шага 2:
(2x + 18)/4 = π + 2πn

Шаг 5: Умножим обе части уравнения на 4, чтобы избавиться от деления:
2x + 18 = 4(π + 2πn)
Распределим 4 на выражение внутри скобок:
2x + 18 = 4π + 8πn

Шаг 6: Выразим x в терминах π и n:
2x = 4π + 8πn - 18
x = (4π + 8πn - 18)/2
x = 2π + 4πn - 9

Теперь у нас есть общее решение уравнения.
Максимально отрицательный корень будет достигаться при минимальном значении n. Так как в уравнении можно использовать любое целое значение n, минимальное значение будет равно -1.

Таким образом, наибольший отрицательный корень равен:
x = 2π + 4π(-1) - 9
x = 2π - 4π - 9
x = -2π - 9