Решите уравнение 9^sinx +9^(-sinx)=10/3
Другие вопросы по теме Алгебра
Популярные вопросы
- Определить процентную концентрацию раствор, полученного при растворении...
1 - Составте план на стихотворение Н.А.Некрасов Железная дорога . По...
2 - Какой объем раствора hcl(d=1.19 г/см3) с массовой долей 38%и сколько...
2 - Как написать адрес человека на английском? Нужен пример, это не...
3 - Придумайте два задания по теме газообмен в легких и тканях в виде...
1 - Приложение 6 сопоставить слова...
2 - Самый короткий доклад Ночь перед Рождеством...
1 - Метод электронного баланса, составьте уравнение реакции. Определите...
3 - 273. Прочитайте. Найдите Слова С Безударными Гласными. Жильцы дома...
2 - 6,3 санды рационал санға айналдыр...
3
Пусть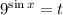 , при этом t>0, получим
, при этом t>0, получим
Домножим левую и правую части уравнения на 3t≠0, получаем
3t² -10t + 3 = 0
D = b² - 4ac = (-10)² - 4 * 3 * 3 = 64;
t₁ = (10+8)/6 = 3
t₂ = (10-8)/6 = 1/3
Возвращаемся к обратной замене