Решите уравнение: 5x^2+y^2+4xy-2x+1=0

В силу того, что каждое из слагаемых неотрицательно, левая часть может равняться нулю тогда и только тогда, когда значение каждого слагаемого равно 0, т.е.

Из первого уравнения легко находится : 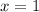. Подставляя его во второе уравнение, находим :

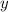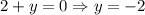
Итак, решением уравнения является единственная пара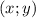 - (1; -2).

ОТВЕТ: (1; -2).