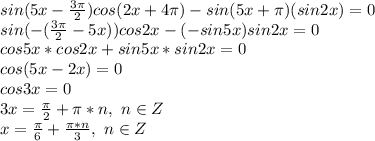Решите уравнение: 1)sin(3pi/2+ x)=1 2)sin(x-pi/2)= 1 3) sin (5x-3pi/2) cos (2x+4pi) - sin (5x+pi)sin2x = 0.
Другие вопросы по теме Алгебра
Популярные вопросы
- Записати заряди йонів у речовині Ba(No3)2...
1 - Порожнисту скляну кульку кинули у воду. Визначте (у відсотках), яку частину об’єму...
2 - Кулю радіуса 12 см перетинає площина,віддалена від її центра на 8см. Знайдіть...
1 - Запишите распределение электронов по ступеням энергии элементов P и Ca....
3 - Определи значения x и y, удовлетворяющие данным условиям:...
1 - 3. Бет 71 8-тапсырма. Көп нүктенің орнына қажетті жалғауды қойып, сөйлемдерді...
2 - Напиши эссе на тему экологическое состояние Караганды...
2 - Атлах шайкасының тарихи маңыздылығы ...
1 - AL и AL3- , CL и CL- чем отличаются данные чистицы по структуре электронов...
1 - Укажіть кількість р-електронів в атомі Сульфуру: а) 5 б) 6в) 8 г) 10 Укажіть...
2
1)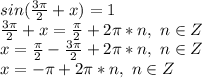
2)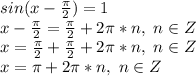
3)