1. Алгебра
  2. Решите систему уравнения подробно

Решите систему уравнения подробно x+y+xy=7
x^2+y^2+xy=13

tarringate tarringate    2   05.04.2021 01:21    10

Ответы
uchenik5713 uchenik5713  05.05.2021 02:25

ответ: (3;1),  (1;3)

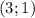Объяснение:

\left \{ {{x+y+xy=7} \atop {x^{2} +y^{2} +xy=13}} \right.  ⇒  \left \{ {{x+y+xy=7} \atop {x^{2} +2xy+y^{2} -xy=13}} \right. ⇒ \left \{ {{x+y+xy=7} \atop {(x+y)^{2} -xy=13}} \right.

Сделаем замену x+y=u;\ \ xy=v;  Тогда:

\left \{ {{u+v=7} \atop {u^{2} -v=13}} \right.

Суммируем оба уравнения и получаем:

u^{2} +u=20;\\u^{2} +u-20=0;\\D=1-4*(-20)=81=9^{2} \\u_{1} =\frac{-1+9}{2} =4;\ \ u_{2} =\frac{-1-9}{2} =-5;

Тогда из равенства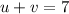 u+v=7 находим v:

v_{1} =7-4=3;\ \ v_{2} =7-(5)=12;

Имеем 2 системы:

1)\ \left \{ {{u_{1} =4} \atop {v_{1} =3}} \right.  и  2)\ \left \{ {{u_{2} =-5} \atop {v_{2} =12}} \right.

Подставляем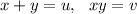 x+y=u,\ \ xy=v и решаем первую систему:

\left \{ {{x+y =4} \atop {xy =3}} \right. ⇒ \left \{ {{y =4-x} \atop {x*(4-x) =3}} \right. ⇒

4x-x^{2} -3=0;\\x^{2} -4x+3=0;\\D=4^{2} -4*3=4=2^{2} ;\\x_{1} =\frac{4+2}{2}=3;\ \ \ x_{2} =\frac{4-2}{2} =1

y_{1} =4-3=1;\ \ \ y_{2}=4-1=3;

Имеем ответы: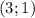 (3;1)  и  (1;3)

Решаем вторую систему:

\left \{ {{x+y =-5} \atop {xy =12}} \right. ⇒ \left \{ {{y =-5-x} \atop {x*(-5-x) =12}} \right. ⇒ -5x-x^{2} -12=0

x^{2} +5x+12=0;\\D=5^{2} -4*12=25-48=-23

Система решений не имеет.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Snezhana200511 Snezhana200511  16.09.2021 02:33
сделайте решением на листочке напишите даю...
сехун2 сехун2  16.09.2021 02:35
Найдите cos a, если sin a=корень из-15/4 и a принадлежит (3п/2; 2п)...
Маруся203 Маруся203  16.09.2021 02:37
№1 Примените формулу: 1) (х+16)(х-16); 2) (3а+0,2)(3а-0,2); 3) (0,1у+0,07)(0,07-0,1у); 4) (-5в-9)(9-5в)...
kydyrali610 kydyrali610  16.09.2021 02:39
Решить по действиям : 6,9 - 4,1*3 + ( 2,1 + 1,3 * 2 ) - (0,3*2 + 0,9 *3)...
Адема12345 Адема12345  16.09.2021 02:41
Реши уравнение: x+3/7=3x-2/2...
vikab4 vikab4  16.09.2021 02:43
0.17. Вычислите: 1) (+0,125 - )) (6,4) 31 +2,5 4,6-2 2,5-1 4,6+2 ) 3 2) 5,2: 0,05 +5,7; 1 0,125 7 3...
Alyonaa201202 Alyonaa201202  16.09.2021 02:44
В первой бригаде из 7 тракторов 2 требуют ремонта, во вто- рой из 5 тракторов 1 требует ремонта. Из каждой бригады наудачу вы- бирают по одному трактору. Определить вероятность того,...
layonel911 layonel911  16.09.2021 02:44
Преобрузуйте в многочлен стандартного вида выражение 1,5(2x-6)+4(x-2)-5(2-3x)...
nadya1801 nadya1801  16.09.2021 02:45
Решите ( ответ с решением )...
savkinaveronika savkinaveronika  13.02.2021 08:56
Реши уравнение 1/7х+22=1/9х-17​...

Популярные вопросы