Решите систему уравнений.
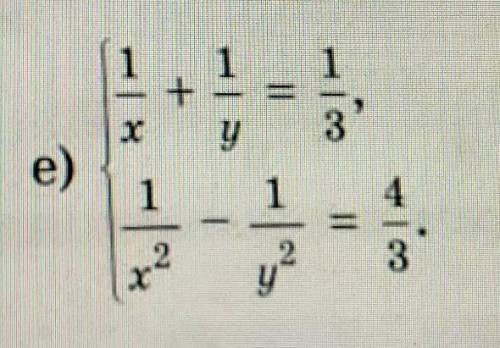
Другие вопросы по теме Алгебра
Популярные вопросы
- Точка дотику кола вписаного в прямокутну трапецію ділить її більшу основу...
1 - Разложите многочлен на множители: 1. 22*18 2. 37*43 3. 54*46 4. 27*13 5....
1 - построить данные векторы умоляю ...
3 - Доведёте тождественность 1) х^6 - у^6=(х-у)(х+у)(х²-ху+у²)(х²+ху+у²)2) (а²+б²)(а^4-а²б²+б^4)-(а³-б³)(а³+б³)=2б^6...
3 - ПОГИТЕЕЕЕ ФИЗИКА ПОДАЛУЙСТА...
2 - Звичайні дроби та дії з ними...
2 - Different people like doing different things. My friend is fond of collecting...
2 - Один из углов треугольника равен 120°. Высота и биссек- триса, проведенные...
3 - Порівняйте повсякденне життя населення україукраїнських земель у XV та XVI...
3 - Заплаканное лицо,сказать что-то,запел о чем-то,ничего не расслышать какой...
2
подставим во второе равенство
Заметим что y≠0
тогда y= -6/11
выразим х
ответ х= 6/13, у= -6/11