Решите систему неравенств: x^2+x-6> 0 x^2-5x-24< =0

x^2+x-6>0

x^2+x-6=0

D= 1^2-4*1*(-6)=24+1=25=5

x1=-1+5/2=2

x2=-1-5/2=-3

чертишь параболу ветви вверх точка выколотая будет от (- бесконечности; до -3) и (от 2; до + бесконечности)

x^2-5x-24<=0

x^2-5x-24=0

D=25-4*1*(-24)= 25+96=121=11

x1=5+11/2=8

x2=5-11/2=-3

парабола ветви вверх точка выолотая будет от (-3:8)

Решаем первое неравенство.

Приравниваем к 0.

Корни урвнения:

Отмечаем на координатной оси и выделяем нужную нам область.

ответ: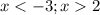 

Решаем второе неравенство.

Снова приравниваем к 0.

Аналогично первому отмечаем на координатной оси.

ответ: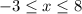 

Объединяем ответы. В итоге получаем ответ: