решите с системы уравнений.расстояние между а и в равно 120 км. из города а в город в вышел автобус, а через 15 мин

Question

Алгебра: решите с системы уравнений.расстояние между а и в равно 120 км. из города а в город в вышел автобус, а через 15 мин – легковая машина, скорость которой больше скорости автобуса на 12 км/ч. легковая машина пришла в город в на 5 мин раньше, чем туда прибыл автобус. найдите скорости автобуса и легковой машины.​

LlesyaLis · Answer

Пусть скорость автобуса равна х км/ч, а скорость легковой машины - у км/ч. По условию, y - x = 12. Тогда время затраченное автобусом равно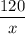 $\dfrac{120}{x}$ , а легковым автомобилем - 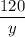$\dfrac{120}{y}$ на весь путь время затрачено 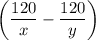$\left(\dfrac{120}{x}-\dfrac{120}{y}\right)$ часов. Зная, что легковая машина пришла в город В на 5 мин раньше, чем автобус, составим систему уравнений

$\displaystyle \begin{cases}&\text{}y-x=12\\&\text{}\dfrac{120}{x}-\dfrac{120}{y}=\dfrac{15+5}{60}\end{cases}~~~\Rightarrow~~~\begin{cases}&\text{}y=x+12\\&\text{}\dfrac{120}{x}-\dfrac{120}{x+12}=\dfrac{1}{3}\end{cases}$