1. Алгебра
  2. Решите показательное неравенство

Решите показательное неравенство с логарифмом.
\displaystyle 5^{\log_x2}\cdot \log_2x+5^{\log_2x}\cdot \log_x2\le 10

КотикОцелотик1 КотикОцелотик1    2   12.12.2019 13:04    1

Ответы
LansWensEEe LansWensEEe  10.10.2020 20:11

5^{\log_x2}\cdot \log_2x+5^{\log_2x}\cdot \log_x2-10\leq0

Рассмотрим функцию: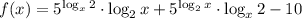 f(x)=5^{\log_x2}\cdot \log_2x+5^{\log_2x}\cdot \log_x2-10

Область определения функции: D(f)=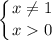\displaystyle \left \{ {{x\ne1} \atop {x0}} \right.

Если 0 < x < 1, то выражение, стоящее слева, будет всегда отрицательным, выполнено.

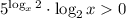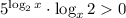Если x > 1, то 5^{\log_x2}\cdot \log_2x0 и 5^{\log_2x}\cdot \log_x20 применимо неравенство Коши (или неравенство о среднем):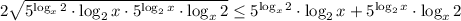 2\sqrt{5^{\log_x2}\cdot \log_2x\cdot 5^{\log_2x}\cdot \log_x2}\leq 5^{\log_x2}\cdot \log_2x+5^{\log_2x}\cdot \log_x2

При этом равенство достигается при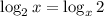 \log_2x=\log_x2 откуда

\log_2^2x=1\\ \\ \log_2x=1\\ \\ x=2

Объединяя решения, получим x ∈ (0;1) ∪ {2}.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
sofiko365 sofiko365  11.06.2019 15:50
Решите уравнение : х + х +10+х-5=215 , так что бы получилось 70.!...
Plild Plild  11.06.2019 15:50
Решить уравнение ,заранее 8х+6=5-3(6х+4)...
liz041 liz041  11.06.2019 15:50
6a+(a/a-2 - a/a+2) / 4a/a^4-2a^3+8a-16, при а=-2,5...
Ромб111 Ромб111  11.06.2019 14:15
Решите неравенство log (4-4x) по осн 2 =log (x^2-4x+3) по осн 2 -log(x+2) по осн 2...
SUPERMOZGgg SUPERMOZGgg  20.08.2019 05:20
Найдите все такие целые cc, при которых дробь c+7c−4c+7c−4 является целым числом. в ответе укажите количество таких целых чисел cc....
RazzyMatem RazzyMatem  20.08.2019 05:20
Решите уравнения: 1) (х-1)*(х+3); 2) (2х-3) во второй степени равно 0...
Infasotka41 Infasotka41  20.08.2019 05:20
Исследовать функцию y=x³-3x² и построить график...
Сашенькадельфинчик Сашенькадельфинчик  01.12.2020 16:01
Найдите 20 член и запишите сумму двадцати первых членов арифметической прогрессии А первое равно 1,3 а2 равно 2,1​...
danilpravdin danilpravdin  01.12.2020 16:01
Запишите используя неравенства утверждения: 1) Сегодня в Ферганской долине температура не выше 20°С2)Вода поднялась на высоту не меньшую 5 м​...
panyaeva06 panyaeva06  01.12.2020 16:02
1)3а²+10а+3=(3а+9)(а+⅓)2)(а+1)(а²+5а+6)=(а²+3а+2)(а+3)​...

Популярные вопросы