Решите оч сложное уровнение !
[tex]7\sqrt[3]{7x-6}=x^{3}+/tex]
Другие вопросы по теме Алгебра
Популярные вопросы
- На автомобиль массой 2 тонны действует сила трения, равная 8...
1 - ОЧЕНЬ ЛЕГКО ЗА Найдите грамматические основы:В углу стоит кровать,...
2 - Решите а то я уже всё забыл нужен 1 правильно решённый пример...
3 - Североамериканские индейцы, показывая на невзрачное растеньице....
2 - Это проверочноя по геометрии решите 3;4;5...
3 - В прямоугольном треугольнике ABCD C равно 90 градусов, А равно...
1 - Как сделать фиолетовый свет ...
2 - органную прелюдию соль минор И.С.Баха. После органной прелюдии,...
2 - В системе координат дан треугольник с вершинами в точках L(4;6),...
1 - Выпиши из предложений вводные слова и вводные сочетания и распредели...
3
Преобразуем это уравнение так, чтобы правая часть превратилась в х:
Рассмотрим функцию![f(x)=\sqrt[3]{7x-6}\\\\](/tpl/images/1021/1608/fc3aa.png) . Если обозначить
. Если обозначить 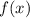 через y, то уравнение
через y, то уравнение ![\sqrt[3]{(7\sqrt[3]{7x-6}-6)}=x\\\\](/tpl/images/1021/1608/96a2b.png) примет вид
примет вид ![\sqrt[3]{7y-6}=x](/tpl/images/1021/1608/cafa7.png) , или
, или 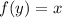 , или
, или 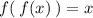
Так как![f(x)=\sqrt[3]{7x-6}\\\\](/tpl/images/1021/1608/fc3aa.png) - возрастающая функция, то согласно теореме:
- возрастающая функция, то согласно теореме:
Если функцияТо есть![\sqrt[3]{7x-6}=x\\\\](/tpl/images/1021/1608/2da17.png) , остаётся только его решить:
, остаётся только его решить:
По теореме, обратной теореме Виета и
и 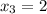
ответ: