Решите логарифмическое ! log1\7(5x+3)≥-1\2
Другие вопросы по теме Алгебра
Популярные вопросы
- Відредагувати речення: 1. У скрутну хвилину друзі кинули його на проізвол....
2 - В выходной день каждый из компании, в которой N друзей, отправил со своего...
1 - Отрезок АВ - диаметр окружности с центром О, АС и СВ - равные хорды этой...
2 - 4.Различают следующее расположение почек на стебле а)очередное , б)супротивное...
1 - У меня есть последниние Также подпишусь СЛУШАТЬ ФРЕДЕРИК ШОПЕН ЗАБЫТЫЙ ВАЛЬС...
3 - Напишите текст на англ м про Украину 7-10 р...
1 - Назвіть країну - дуалістичну монархію. Які у неї зв’язки з Україною?...
1 - 18:05Математика1-жаттығуЕгер x = -3,5 болса, өрнектің мәнін тап |x|.Жауабы:...
1 - 13. Составь и запиши текст о городе будущего. Используй понра-вившиеся опорные...
3 - Решите нормально время 20 мин На некоторых деревьях в волшебном лесу растут...
1
log1\7(5x+3)≥-1\2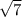 )
)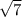 )
)
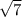 ≥(5х+3)
≥(5х+3)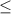 0 ; 25х^2+30x+2
0 ; 25х^2+30x+2 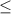 0
0
log по основанию к 7^-1 числа (5х+3)≥-1\2
1/(-1) log по основанию к 7 числа (5х+3)≥-1\2
-1 log по основанию к 7 числа (5х+3)≥-1\2
log по основанию к 7 числа (5х+3)^-1 ≥-1\2
(5х+3)^-1 ≥ (1/
1/(5х+3) ≥ (1/
возв в квадрат, получаем:
7 ≥ 25х^2+30x+9; 25х^2+30x+9-7
Решаем методом интервалов и получаем ответ