Алгебра: решить уравнения типа sinx=a

решить уравнения типа sinx=a

Ответы

Urtaol20 13.09.2020 11:26

1) 5sinx =3 ⇔ sinx = 0,6 ⇒ x = (-1)ⁿarcsin(0,6) +πn , n ∈ ℤ .

2) 1 - 2sinx = 0⇔ sinx = 1/2 ⇒ x = (-1)ⁿπ/6 +πn , n ∈ ℤ .

3) 4sinx +5 =0 ⇔ sinx = -1,25 ⇒ x ∈ ∅ . не имеет решения | sinx | ≤ 1

4) 2sin(3x +π/3) + √3 =0 ⇔sin(3x +π/3) = -(√3) /2 ⇒

3x+ π/3 = (-1) ⁿ⁻¹ π/3 + πn ⇔ (совокупность _ИЛИ )

[ 3x+ π/3 = - π/3 + π*2k ; 3x+ π/3 = π/3 + π*(2k+1) , k ∈ ℤ ⇔

[ x = - 2π/9 + (2π/3)k ; x= (π/3)(2k+1) , k ∈ ℤ

5) 12sin(x/4 -π/6) -12 =0 ⇔sin(x/4 -π/6) =1 ⇒ x/4 -π/6 =π/2 +2πk ,k ∈ ℤ ⇔

x = 8π/3 +8πk ,k ∈ ℤ

6) (2sin4x - 4)(2sinx+1) =0 ⇔ (sin4x -2)(sinx +1/2) = 0 ||sin4x ≠2 || ⇔

sinx +1/2 =0 ⇔sinx = -(1/2) ⇒ x =(-1) ⁿ⁻¹ *(π/6) + πn , n ∈ ℤ

7) sin(x/2)cos(x/3) -cos(x/2)sin(x/3) =0⇔sin(x/2 - x/3) =0 ⇔sin(x/6) =0 ⇒

x/6 =πn , n ∈ ℤ ≡ x = 6πn , n ∈ ℤ

8) 4sin3x*cos3x - √2 =0 ⇔ 2sin(2*3x) - √2 =0 ⇔sin(6x) =(√2)/2 ⇔

6x =π/4 +πn , n∈ℤ ⇔ x = π/24 +(π/4)*n , n∈ℤ

ПОКАЗАТЬ ОТВЕТЫ

макс10710 13.09.2020 11:26

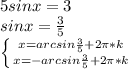
1) $5sin x =3\\ sin x=\frac{3}{5} \\ \left \{ {{x=arcsin\frac{3}5+2\pi*k} } \atop {x=-arcsin\frac{3}5+2\pi*k}} \right.$

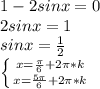
2) $1-2sinx=0\\2sinx=1\\sinx=\frac{1}{2}\\\left \{ {{x=\frac{\pi}{6}+2\pi *k } \atop {x=\frac{5\pi}{6}+2\pi *k}} \right.$

3) $4sin x +5=0\\sin x=-\frac{5}{4} \\\\$

нет ответа т.к. -5/4 <-1

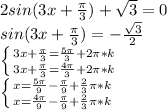
4) $2 sin(3x+\frac{\pi}{3} )+\sqrt{3}=0\\sin(3x+\frac{\pi}{3} )=-\frac{\sqrt{3}}{2} \\\left \{ {{3x+\frac{\pi}{3} =\frac{5\pi}{3}+2\pi *k } \atop {3x+\frac{\pi}{3} =\frac{4\pi}{3}+2\pi *k}} \right. \\\left \{ {{x =\frac{5\pi}{9}-\frac{\pi}{9}+\frac{2}{3} \pi *k } \atop {{x =\frac{4\pi}{9}-\frac{\pi}{9}+\frac{2}{3} \pi *k}} \right.$

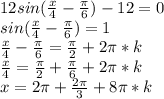
5) $12sin(\frac{x}{4}-\frac{\pi}{6})-12=0\\sin(\frac{x}{4}-\frac{\pi}{6})=1\\\frac{x}{4}-\frac{\pi}{6}=\frac{\pi}{2}+2\pi *k\\ \frac{x}{4}=\frac{\pi}{2}+\frac{\pi}{6}+2\pi *k\\x=2\pi+\frac{2\pi}{3}+ 8\pi *k\\$

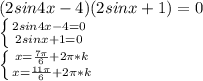
6) $(2sin4x-4)(2sinx+1)=0\\\left \{ {2sin4x-4=0} \atop {2sinx+1=0}} \right. \\\left \{ {{x=\frac{7\pi}{6} +2\pi * k} \atop {x=\frac{11\pi}{6} +2\pi * k}} \right.$

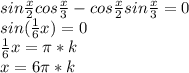
7) $sin\frac{x}{2}cos\frac{x}{3}-cos\frac{x}{2} sin\frac{x}{3}=0\\ sin(\frac{1}{6}x )=0\\\frac{1}{6} x=\pi *k\\x=6\pi*k$

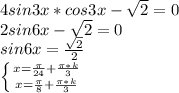
8) $4sin 3x*cos3x-\sqrt{2} =0\\2sin 6x -\sqrt{2}=0\\sin 6x = \frac{\sqrt{2}}{2}\\\left \{ {{x=\frac{\pi}{24}+\frac{\pi * k }{3} } \atop {{x=\frac{\pi}{8}+\frac{\pi * k }{3} }} \right.$