Решить тригонометрическое уравнение:
8cos(x)^2+6sin(x)-3=0
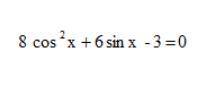
Другие вопросы по теме Алгебра
Популярные вопросы
- 300 за полный две бригады работая совместно с одинаковой производительностью изготавливают...
2 - Вбиосинтезе полипептида участвовали т-рнк с антикадонами ууа, ггц, цгц, ауу, цгу....
1 - Витя придумал 6 выражений со скобками, значение которых равно 15, а лена придумала...
1 - Отрицательные качества карла великого...
1 - Существовала легенда, что римскую христианскую общину создал сам апостол петр. а...
2 - 2класс информатикарозгадай ребус и дизнайся про улюблену розваг у смайлика буква...
3 - Дано. m(so2)=6,4 г v(so2)=? m(so2)=? m(so2)=?...
3 - Встречают хлебом солью а провожают как?...
1 - Вячейке электронной таблицы а1 записана формула =$d1+d$2. какой вид приобретет формула,...
3 - Как найти перимитр,и площадь в ? : длина коридора прямоугольной формы. 6м ,а ширина...
2
решений нет
Объяснение:
8cos²x+6sinx-3=0
8(1-sin²x)+6sinx-3=0
-8sin²x+6sinx+ 5=0 ,
8sin²x-6sinx- 5=0 , пусть sinx=а , |a|<1
8а²-6а-5=0 , Д=36+160=196 ,
а₁ =(6-14):2=-4 не подходит под условие |a|<1
, а₂=(6+14):2=10 не подходит под условие |a|<1