Решить систему уравнений
x-1=-1
y^2-7x=7

x-1=-1               система

y^2-7x=7

x=0                   система

y^2-7x=7

y^2-7*0=7

y=-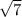

y=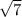

(x1,y1)=(0,-)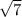

(x2,y2)=(0,)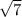

0-1=-1                   система

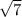(-)^2-7*0=7

0-1=-1                    система

^2-7*0=7

-1=-1                     система

7=7

-1=-1                    система

7=7

(x1,y1)=(0,-)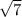

(x2,y2)=(0,)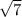

Объяснение

ответ: (0;√7); (0;-√7)

Объяснение:

из первого уравнения. х=-1+1=0

подставим во второе. получим у²-7*0=7, откуда у=±√7

имеем два решения (0;√7); (0;-√7)