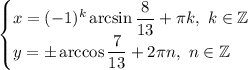Решить систему уравнений
{3sinx+4cosy=4
2sinx+7cosy=5
Другие вопросы по теме Алгебра
Популярные вопросы
- Составит маленький фантастический рассказ...
1 - А)Какое расстояние проползет улитка за ¾ часа, если его скорость равно 24/25 метр./мин....
2 - У танцювальному гуртку 55%усіх учнів становлять дівчата. Скільки дівчат і скільки...
1 - напишите эл. письмо другу о фильме который недавно посмотрел . на английском языке....
3 - Складіть рівняння реакцій за схемою: етен- етін- бензен- циклогексан бензен- 1,2,3,4,5,6-гексахлорциклогексан....
1 - Напишите сочинение на тему если бы я был главой района !!...
3 - Назвіть переваги та недоліки автомобільного транспорту...
3 - если лень все решать, натолкните хотя бы на мысль ...
3 - Ребят написать текстовое сообщение на две страницы по 10 теме...
2 - Алюмінієвий дріт діаметром 2,4 мм має масу 1 кг. Обчисли довжину дроту, якщо щільність...
3
Первое уравнение домножим на 2, а второе - на (-3):
Складываем уравнения:
Теперь в исходной системе первое уравнение домножим а 7, а второе - на (-4):
Складываем уравнения:
ответ: