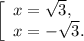X^4+6x^2-27=0 развернутое решение плз
Другие вопросы по теме Алгебра
Популярные вопросы
- Напишите 10 предложений на тему как мы с семьёй провели пасху...
1 - Обьясни как составлена последовательностб чисел : 3, 12, 48, 192,...
2 - Ca, al, ge, p,se имеет два не спаренных электрона...
1 - Расскажи о каком-нибудь известном человеке который когда-то жил...
2 - Прочитай фразу на языке. выбери фразу на языке, которая описывает...
3 - Если площадь прямоугольника равна 4 дм в квадрате, а его ширина...
1 - Написать эссе на тему путешествие гулевера ?...
2 - 21/3 + 37 -2 1/3 это дробь. знаю, что пример лёгкий, но решить...
2 - Масса книг в одной упаковке равен 15кг сколько книг в одной упаковке...
2 - 3предложения со словом священный и 3 предложения со словом свещенный...
1
Объяснение:
Данное уравнение является биквадратным. Решаем путем замены. Пусть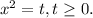
Тогда уравнение принимает вид:
t=-9 не удовлетворяет условию . Значит t=3.