Решить систему методом сложения 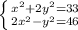
Другие вопросы по теме Алгебра
Популярные вопросы
- Морфология бойынша жиынтық бақылау, білім ленд не пиши те всякую фигню,мне...
2 - Дисциплина в монгольском войске держалась на «Казахстан ва) преданности...
3 - Что означают понятие железы, секреция, секреты...
1 - Вычислить объем куба по формуле : V=в3, если в=4х-5...
2 - Задание №3. Выпишите местоимения, распределите их по разрядам. Определите...
2 - Завершение процесса формирования казахского народа. Урок 2 Соотнеси источник...
2 - При каких значениях m уравнения будут равносильны? 4x-7=9 и x+5m=-9?...
3 - Кестены толтыр 9 сабак 3 сынып 1 топсырма...
3 - Лист другу на тему мой любимый журнал ...
1 - Можете с СОРОМ по русскому языку...
1
Объяснение:
Суммируем эти уравнения:
ответ: (-5;-2), (-5;2), (5;-2), (5;2).
ответ: x1,2=±5. y1,2=±2.
Объяснение:
x^2+2y^2=33; (1)
2x^2-y^2=46; [*2] (2)
4x^2-2y^2=92; (3)
Складываем (1) и (3)
x^2+2y^2=33;
4x^2-2y^2=92;
x^2+4x^2=33+92;
5x^2=125;
x^2=25;
x1,2=±5.
x1=5 подставляем в (2):
2*5^2-y^2=46;
50-y^2=46;
-y^2=46-50;
-y^2=-4;
y1,2=±2.
x2=-5 подставляем в (2)
2*(-5)^2-y^2=46;
50-y^2=46;
-y^2=46-50;
-y^2=-4;
y3,4=±2.