Решить систему алгеброического сложения
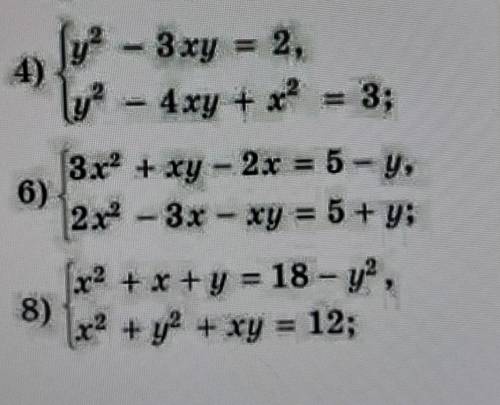
Другие вопросы по теме Алгебра
Популярные вопросы
- да 30 катя и коля живут в одном доме. из дома в школу вышла катя...
2 - Вдетском мире продавали двухколесные и трехколесные велосипеды...
3 - Вбуфете тарелок было в 4 раза больше , чем на столе . когда на...
2 - Сделать фонетический разбор слова высокие...
2 - Что общего у животных: розовая чайка, паук-птицеед, карликовый...
3 - Водном мешке лежало 205 яблок,в другом-сколько же.сколько яблок...
3 - Почему плавает корабль? что его держит? объяснение, пояснение...
2 - Какой изложение примерно будит вы 4 февраля...
2 - Які квіти ростуть у лісах твоєї місцевості 5-7 речень (про одну...
2 - Отношение а: b равно 8: 9. найдите отношение 9а: 4b....
3
4)
{ y^2 - 3xy = 2
{ y^2 - 4xy + x^2 = 3
Умножаем 1 уравнение на -1:
{ -y^2 + 3xy = -2
{ y^2 + x^2 - 4xy = 3
Складываем уравнения:
x^2 - xy = 1
y = (x^2 - 1)/x = x - 1/x
Подставляем в 1 уравнение:
(x - 1/x)^2 - 3x(x^2 - 1)/x - 2 = 0
x^2 - 2x*1/x + 1/x^2 - 3x^2 + 3 - 2 = 0
-2x^2 - 2 + 1/x^2 + 1 = 0
Умножаем всё на x^2 и на -1, избавляемся от дробей:
2x^4 - x^2 - 1 = 0
(x^2 -1)(2x^2 + 1) = 0
2x^2 + 1 > 0 при любом x, поэтому эту скобку можно удалить:
x^2 - 1 = 0
x1 = -1; y1 = x - 1/x = -1 - 1/(-1) = -1 + 1 = 0
x2 = 1; y2 = x - 1/x = 1 - 1/1 = 0
ответ: (-1; 0); (1; 0)
6)
{ 3x^2 + xy - 2x = 5 - y
{ 2x^2 - xy - 3x = 5 + y
Складываем уравнения
5x^2 - 5x = 10
Делим все на 5 и переносим налево
x^2 - x - 2 = 0
(x+1)(x-2) = 0
x1 = -1
3(-1)^2 - 1y - 2(-1) = 5 - y
3 - y + 2 = 5 - y
5 = 5
Это верно при любом y.
x2 = 2
3*4 + 2y - 2*2 = 5 - y
12 + 2y - 4 = 5 - y
3y = 9 - 12 = -3
y = -1
ответ: 1) x1 = -1; y1 - любое; 2) x2 = 2; y2 = -1
8)
{ x^2 + x + y = 18 - y^2
{ x^2 + y^2 + xy = 12
В 1 уравнении перенесем y^2 влево. 2 уравнение умножим на -1:
{ x^2 + y^2 + x + y = 18
{ -x^2 - y^2 - xy = -12
Складываем уравнения:
x + y - xy = 18 - 12 = 6
y(1 - x) = 6 - x
y = (6-x)/(1-x)
Подставляем в 1 уравнение:
Домножаем всё на знаменатель, избавляемся от дробей:
x^2(1-x)^2 + (6-x)^2 + x(1-x)^2 + (6-x)(1-x) - 18(1-x)^2 = 0
x^2(1-2x+x^2) + 36 - 12x + x^2 + x(1-2x+x^2) + 6 - 7x + x^2 - 18(1-2x+x^2) = 0
x^2 - 2x^3 + x^4 + 36 - 12x + x^2 + x - 2x^2 + x^3 + 6 - 7x + x^2 - 18 + 36x - 18x^2 = 0
x^4 - x^3 - 17x^2 + 18x + 42 = 0
Это уравнение имеет 4 иррациональных корня.
x1 ≈ -3,87; y1 = (6-x)/(1-x) ≈ 2,026
x2 ≈ -1,19; y2 = (6-x)/(1-x) ≈ 3,283
x3 ≈ 2,71; y3 = (6-x)/(1-x) ≈ -1,924
x4 ≈ 3,36; y4 = (6-x)/(1-x) ≈ -1,119
Похоже, в системе опечатка. Слишком сложно по сравнению с 4) и 6).