решить один интеграл, очень Под номером 15
От что есть
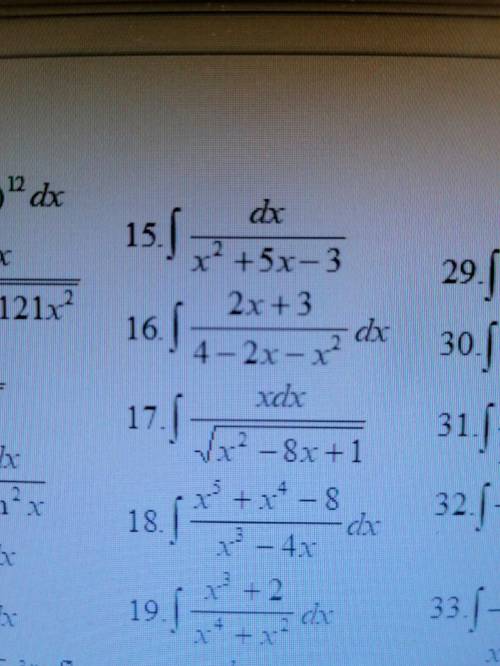
Другие вопросы по теме Алгебра
Популярные вопросы
- Яку кінетичну енергію придбае електрон, якщо він пролетить між двома точками,...
1 - 3. 1) Позначити на координатній площині точки А(-2; 2); В(1; -4); M(3; 4)....
1 - 6 и 7 или 8 срмзчїгазазгагзящгвгз...
3 - Чиста культура певного виду мікроорганізмів, у якої вивченіморфологічні та...
1 - У трикутнику ABC знайдіть сторону AC, якщо 2B-30°, 2С-45°, сторона AB дорівнює...
3 - Народ ответить на вопросы по свч все вопросы...
2 - 11. После революции 1848 года в Германии: A) к власти пришел Вильгельм IB)...
2 - Дана прямоугольная матрица размерности MxN [0,100]. Сформировать одномерный...
3 - Докази які підтверджують гумористичність повісті Вітька + Галька...
1 - Задача 3. Визначити тиск кисню в балоні, якщо при температурі Т = 250 к середнятривалість...
1
Выделим в знаменателе квадрат суммы:
Когда подставим это в интеграл, можно будет заметить в нем табличный:
Получаем: