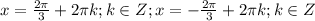Решить на пробном егэ cos2x-sin(pi\2+x)=1+ctgx*tg(pi-x)
Другие вопросы по теме Алгебра
Популярные вопросы
- 4. Прочитайте текст ещё раз. Нарисуйте предложенный кластер в тетради....
3 - Определите силу тяжести, действующую на тело (см. рисунок) Решите через...
3 - Сколько будет. 663647747474753858588585858•4664646464566546565664554...
1 - из 2 городов на встречу друг другу одновременно вышли 2 поезда скорость...
3 - мне решить задачу если решите мне это правильноя вам поставлю лайк❤️...
3 - ПАЖЭ Знаю много но на кону мая жызнь ☠️...
2 - Read the text about advertising and decide if the statement is True,...
1 - Определи дееприч обороты из предложения ...
2 - Преобразование (трансформация) и декорирование швейных изделий. Урок...
3 - Решите уравнение 1/2х=11 Варианты ответа Нет корней225,5Множество корней...
2
Область определения уравнения:
Не удовлетворяет области определения.
ответ: