1. Алгебра
  2. Решить .хотя бы 1 .буду признательна

Решить .хотя бы 1 .буду признательна за ответ. 1.исследуйте функцию , постройте график. 2. найдите количество действительных корней уравнения: 3. найдите найбольшее значение фунцкции на промежутке [1; 3].

lawrence02 lawrence02    2   29.03.2019 15:00    0

Ответы
vanyadrachuk2004 vanyadrachuk2004  27.05.2020 13:03

3 задание.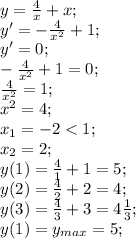 y=\frac{4}{x}+x;\\ y'=-\frac{4}{x^2}+1;\\ y'=0;\\ -\frac{4}{x^2}+1=0;\\ \frac{4}{x^2}=1;\\ x^2=4;\\ x_1=-2<1;\\ x_2=2;\\ y(1)=\frac{4}{1}+1=5;\\ y(2)=\frac{4}{2}+2=4;\\ y(3)=\frac{4}{3}+3=4\frac{1}{3};\\ y(1)=y_{max}=5;

2задание

6+36x-3x^2-2x^3=0;

 Так как важно количевство!

Кубическое уравнение имеет не более 3 действительных корней

y(x)=6+36x-3x^2-2x^3;\\ y(-6)=6+36*(-6)-3*(-6)^2-2*(-6)^3=1140;\\ y(-4)=6+36*(-4)-3*(-4)^2-2*(-4)^3=-314<0;\\ -6<x_1<4;\\ y(-1)=6+36*(-1)-3*(-1)^2-2*(-1)^3=-31<0;\\ y(0)=6+36*0-3*0^2-2*0^3=60;\\ -1<x_2<0;\\ y(3)=6+36*3-3*3^2-2*3^3=330;\\ y(4)=6+36*4-3*4^2-2*4^3=-26<0;\\ 3<x_3<4;

значит данное кубическое уравнение имеет 3 действительных корня

 

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
shubinaale shubinaale  27.04.2020 11:28
У геометричній прогресії п ятий член дорівнює 25 ,а шостий становить 125.Чому дорівнює другий член прогресії?...
nicgames nicgames  27.04.2020 10:49
Контрольная работа №7 по теме «Системы линейных уравнений с двумя переменными» 1 вариант Мерзляк...
Диарочка1 Диарочка1  27.04.2020 10:41
Корни х1 и х2 уравнения х^2+6х+с=0 удовлетворяют условию х1 - 3х2 = 22. Найти корни уравнения и значение с...
Masterpro123 Masterpro123  07.12.2020 15:46
Найти абсолютную погрешность вычисления числа 0,1678 числом 0,168 2. Записать в виде двойного неравенства х=14+(-)0,3 3. Округлить 11,45 с недостатком и с избытком. Найти...
KYRT2 KYRT2  07.12.2020 15:48
сделай замену, чтобы получить квадратное уравнение 3(x-7)^4+(x-7)^2-8=0сделаем замену t=(x-7)^2=0что сюда ставить? ​...
vikavika1417 vikavika1417  07.12.2020 15:48
Решите систему уравнений графическим 2x + y = 5.​...
ника2346олл ника2346олл  07.12.2020 15:49
1.подайте число в стандартному вигляда 1)5201,42)0,231×10(-2)3) 0,002814) 731,5×10(-5)​...
StalinReal StalinReal  07.12.2020 15:50
Друзья,сколько будет xa:ty?...
SERYK11 SERYK11  07.12.2020 15:51
Решите систему уравнений графическим х решение и обьяснение.​...
katemur6969 katemur6969  07.12.2020 15:51
Найдите область определения функцииy=6/3-2х​...

Популярные вопросы