решить эти 2 номера!! Объясните очень понятно, потому что я даже в интернете искал, но ничего не понятно
Другие вопросы по теме Алгебра
Популярные вопросы
- Если бы земля имела форму конуса или цилиндра смогли ф.магеллан совершить путешествие...
2 - 1. do you have a healthy diet? 2. what exercise do you do? 3. do you often feel...
1 - Периметр правильного треугольника равен 48 корень из 3. найдите длину высоты....
1 - Сколько в солнечной системе планет, и назовите их...
2 - Докажите что в равных треугольниах медианы...
2 - Мне нужно написать сочинение почему нельзя драться ,накидайте примерчиков,буду...
2 - 1. непосредственно в сборке молекул белка участвуют : клеточная мембрана наружная,...
1 - Звук вечер дорогая берег во всех этих словосочетаниях пропущенные прилагательные...
2 - Чому дорівнюєє радіус кола описаного навколо квадрата зі стороною 8см?...
1 - Вначале года в городе проживало 600 тыс. чел. к концу года численность населения...
1
Відповідь:
Пояснення:
1)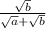
2)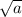
Объяснение:
1)
2)