решить. Для контрольной работы 1) Интеграл от точки 0 до Пи/12 (1-cos2x)dx
2) интеграл от точки 0 до 2 (1+2x)dx
Ответы
Задание 1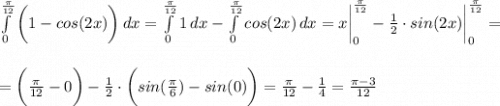 Задание 2
Задание 2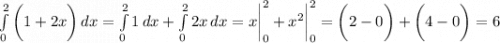
ПОКАЗАТЬ ОТВЕТЫ
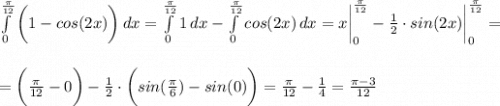 Задание 2
Задание 2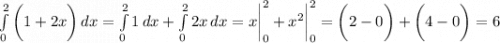
Другие вопросы по теме Алгебра
Популярные вопросы
- отрезок cd перпендикулярный плоскости треугольника abc ,угол abc=90°,dc=7см,da=db=11см,найти...
3 - НАПИСАТЬ ЭССЕ НА ТЕМУ ЖИЗНЬ В СЕМЬЕ соблюдать план1выступление2основная часть это...
2 - Найдите верное утверждение А) По значению причастия делиться на действительные...
2 - Рассчитайте массу воды ,необходимую для приготовления 20-процентного раствора массой...
1 - С ФИЗИКОЙ, ОТ С ДАНО И РЕШНИЕМ 1.В брусок массой 500 г, лежащий на столе, попадает...
3 - Көмектесіңдерші өтінем қатты керек болып тұр...
1 - Аралас сандарды қосу. Аралас сандарды азайту. 6-сабақ C нүктесі AB кесіндісін екі...
3 - СДАВАТЬ ЧЕРЕЗ 30 МИНУТ У МЕНЯ 59последний пример7)х/8 + у/2 - 3 при х=5, у=3...
2 - Номер Дано доказательство...
1 - Герой нашего времени Чем обидел Печорин Максима Максимыча во время их последней...
2