решить 3.Преобразуйте выражение в одночлен стандартного вида:
1)-3 x(в 3 степени)y(в 4 степени) x(в 5 степени)×4y(в 3 степени)
2) (-4a(в 6 степени)b)(все в 3 степени)
4.Представте в виде многочлена стандартного вида выражение:
Не понятно пишите)
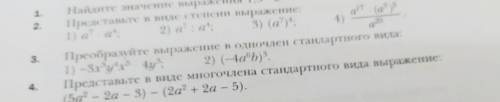
Ответы
Хорошо, я распишу и объясню каждый шаг решения для вас.
1) Решение первого выражения:
Для преобразования в одночлен стандартного вида, нужно объединить все переменные одного типа и соответствующие им степени.
Итак, у нас дано выражение: -3x^3y^4x^5 * 4y^3
Сначала перемножим числа без переменных:
-3 * 4 = -12
Теперь перемножим переменные со схожими основаниями (x и y) и сложим степени:
x^3 * x^5 = x^(3+5) = x^8
y^4 * y^3 = y^(4+3) = y^7
Объединяя все вместе, получаем искомый одночлен стандартного вида:
-12x^8y^7
2) Решение второго выражения:
Теперь рассмотрим второе выражение: (-4a^6b)^3
Нам нужно возвести всю скобку в третью степень.
Используем формулу (a^m)^n = a^(m*n):
(-4a^6b)^3 = -4^3(a^6)^3*(b^3)^3
Возводим каждый множитель в скобках в третью степень:
-4^3 = -64
(a^6)^3 = a^(6*3) = a^18
(b^3)^3 = b^(3*3) = b^9
Объединяем все, чтобы получить многочлен стандартного вида:
-64a^18b^9
3) Представление выражения в виде многочлена стандартного вида:
На картинке дано выражение: (2x^3y^2 - 3xy)^2 + x^2(y^2 - 4x^3y)
Нам нужно раскрыть скобки и упростить выражение.
(2x^3y^2 - 3xy)^2 = (2x^3y^2 - 3xy) * (2x^3y^2 - 3xy)
Для упрощения выражения, умножим эти две скобки с помощью правила дистрибутивности:
(2x^3y^2 - 3xy) * (2x^3y^2 - 3xy) = (2x^3y^2 * 2x^3y^2) + (2x^3y^2 * -3xy) + (-3xy * 2x^3y^2) + (-3xy * -3xy)
Умножим каждое слагаемое:
(4x^6y^4) + (-6x^4y^3) + (-6x^4y^3) + (9x^2y^2)
Теперь раскроем вторую скобку:
x^2(y^2 - 4x^3y) = x^2y^2 - x^2(4x^3y)
Умножим каждое слагаемое:
x^2y^2 - 4x^5y^3
Итак, теперь сложим все слагаемые:
(4x^6y^4) + (-6x^4y^3) + (-6x^4y^3) + (9x^2y^2) + x^2y^2 - 4x^5y^3
Группируем по типам переменных и складываем:
4x^6y^4 - 12x^4y^3 + 10x^2y^2 - 4x^5y^3
Таким образом, искомое представление в виде многочлена стандартного вида:
4x^6y^4 - 12x^4y^3 + 10x^2y^2 - 4x^5y^3
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Популярные вопросы
- Вычислите произведение 1/3 и числа , обратного 6. Вичислите произведение...
1 - решить: Выполните деление 9-2p/8n²:9-2p/4nупростите выражение 14/28x²-7xy•(4x-y)Возведите...
1 - Придумайте два любых числовых множества. Найдите объединение и...
2 - Сучасна філософська думка в Україні розвивається у напрямах: а)...
3 - Упр 423а,русский язык, хелп...
1 - Как ты думаешь Зачем нужны звёзды на небе кто зажигает их почему...
1 - Подготовить сообщение о любом море....
3 - Сделайте кроссворд на тему 10 птиц Удмуртии умоляю....
3 - Криптон у початковому стані за тиску 200 кПа займає об’єм 5 л....
2 - На двух садовых участках имеется 64 куста малины. Если с первого...
2