1. Алгебра
  2. Реши квадратное уравнение 2(4x−9)2−9(4x−9)+4=0

Реши квадратное уравнение 2(4x−9)2−9(4x−9)+4=0

(первым вводи больший корень):
x1=___; x2= ___;
.

Дополнительный во какой метод рациональнее использовать?

Метод введения новой переменной
Разложение на множители
Раскрытие скобок
Вынесение за скобку

vakumm765 vakumm765    2   12.03.2020 08:32    0

Ответы
irochka320969 irochka320969  11.10.2020 21:18

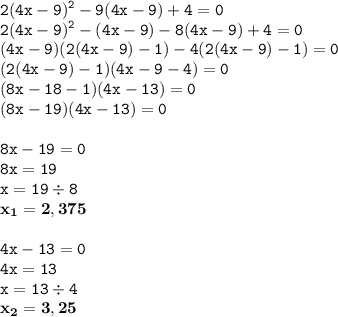
\displaystyle \tt 2(4x-9)^2-9(4x-9)+4=0\\\displaystyle \tt 2(4x-9)^2-(4x-9)-8(4x-9)+4=0\\\displaystyle \tt (4x-9)(2(4x-9)-1)-4(2(4x-9)-1)=0\\\displaystyle \tt (2(4x-9)-1)(4x-9-4)=0\\\displaystyle \tt (8x-18-1)(4x-13)=0\\\displaystyle \tt (8x-19)(4x-13)=0\\\\ \displaystyle \tt 8x-19=0\\\displaystyle \tt 8x=19\\\displaystyle \tt x=19\div8\\\displaystyle \tt \bold{x_1=2,375}\\\\\displaystyle \tt 4x-13=0\\\displaystyle \tt 4x=13\\\displaystyle \tt x=13\div4\\\displaystyle \tt \bold{x_2=3,25}

ответ: \displaystyle \tt x_1=2,375;\: \: x_2=3,25

ответ на вопрос:

Я считаю, что здесь удобнее использовать метод вынесения общего множителя за скобки.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
annaegoshina annaegoshina  19.11.2020 15:52
В треугольнике ABC сторона AB равна 4 см, высота CM, проведённая к данной стороне, равна 11 см. В треугольнике проведена медиана AN....
darinakor140197nooii darinakor140197nooii  19.11.2020 15:52
Переведи скорость в указанные единицы измерения. Результат округли до единиц. 311 м/с = м/мин 311 м/с = см/с...
Miniplayer Miniplayer  19.11.2020 15:52
Решите графически систему уравненияy=-xy=2-3x​...
ашоттрубошот ашоттрубошот  19.11.2020 15:43
Lim(n/4n+3) стремится к бесконечности...
elenabuda85 elenabuda85  19.11.2020 15:40
Напишите: область определения, область значений, промежутки монотонности, разрывы, минимумы и максимумы для следующих функций: 1. у=х2+1 2. у=1/(х2-1) 3. у=√(7-2х)​...
КсенияВиленская КсенияВиленская  08.09.2019 02:30
|х-1|=25 уравнение с модулем решите...
leontievasv leontievasv  08.09.2019 02:30
Решить уравнение-3(5+2х)-7 (х-4)+5=18...
nikzakora nikzakora  08.09.2019 02:30
16 октября работа 1. подобные слагаемые: а) 7х - 3х+х = б) 4а -3 +5а +4 +а = в) 2х -3у +1 +2х +5у -6х= г) 2а +а +2в -4а -4в +7= д) 5х + 7 -3х +3= 2.раскройте скобки:...
Ardak123 Ardak123  08.09.2019 02:30
Sin^3 x + cos^3 x = -1 сколько у него решений на промежутке [0: 6pi] ( можете дать ответ на листке или что бы было понятно )...
krllzrbn442 krllzrbn442  08.09.2019 02:30
Раскрой скобки и подобные слагаемые: 4(2,4−1,8a)+9a−11,9=...

Популярные вопросы