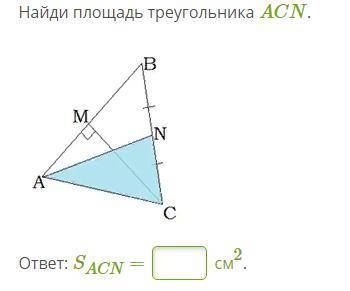
В треугольнике ABC сторона AB равна 4 см, высота CM, проведённая к данной стороне, равна 11 см. В треугольнике проведена медиана AN.
Другие вопросы по теме Алгебра
Популярные вопросы
- Выполни деление на натуральное число (Запиши правильную несократимую...
1 - Fe-FeCl2-Fe(OH)2-Fe(OH)3-Fe(NO3)3 генетическую цепочку ...
1 - 510. Для ремонту будинку запросили кількох робітників. Якщо їх буде...
1 - 602. а) На сколько процентов число 32 меньше 40? б) На сколько процентов...
3 - Е) 450-130 - 3 5. Реши задачу.а) Туристы посетили водопад и озеро....
2 - Выбери верный ответ. Первый столяр каждые 3 ч делает по 72 деревянные...
2 - Будь ласка напишіть письмовий твір розповідного характеру з елементами...
1 - 7. Определите, к какому царству относится данный живой организм...
1 - Подберите однокоренные глаголы слова ненавидеть и кантование недоумение...
1 - Умоляю нужна ! 1. Чи вважаєте ви фантастичними оповідями історії...
1
Первое, что нам нужно сделать, это найти длину стороны AM. Мы знаем, что CM - высота треугольника, и она перпендикулярна стороне AB. Это означает, что AM является средней линией треугольника и делит сторону AB пополам. Так как AB равна 4 см, длина AM будет равна половине этого значения, то есть 2 см.
Теперь, чтобы найти длину стороны AN, мы можем воспользоваться теоремой Пифагора. Так как AM и CM являются прямыми углами, то треугольник AMC является прямоугольным треугольником. Мы знаем, что AM = 2 см, и CM = 11 см. Используя теорему Пифагора, можем вычислить длину стороны AC:
AC² = AM² + CM²
AC² = 2² + 11²
AC² = 4 + 121
AC² = 125
Теперь найдем квадратный корень из 125, чтобы найти длину стороны AC:
AC ≈ √125 (примерно равно)
AC ≈ 11.2 см (округляем до одного знака после запятой)
Так как сторона AC равна 11.2 см, то сторона AN также будет равна 11.2 см, так как AN является медианой, и медиана делит сторону AB пополам.
Ответ: Длина стороны AN равна примерно 11.2 см.