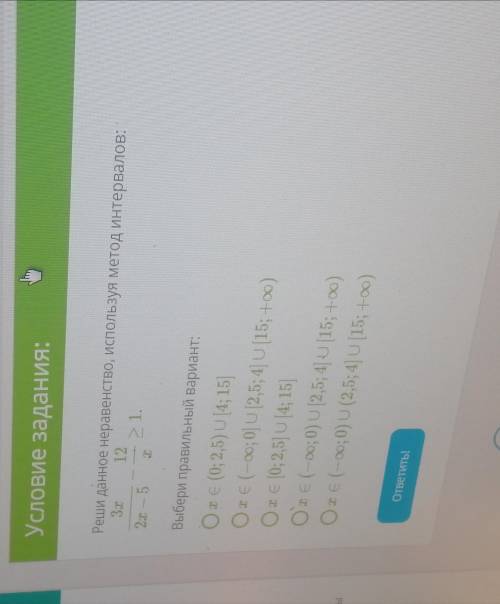
Реши данное неравенство используя метод интервалов :
Другие вопросы по теме Алгебра
Популярные вопросы
- Роль в составлении нового стиля 18 века...
1 - Скакими из в-в будет взаимод. соляная кислота: медь,оксид висмута (iii),гидроксид...
1 - 939. груз какой массы надо подвесить к пружине с жестстью 240 н/м, чтобы он...
3 - Одна сторона треугольника на 2см короче чем вторая и в 2 раза короче чем третья....
2 - Вящике 15 белых, 10 красных и 8 желтых яблок. не возвращая вящикиоттуда последовательно...
1 - Решить уравнение с модулем. -4*|x^2 - 1| - 3 = 1/ x^2 - 1....
1 - Напиши известные части речи. у меня тогда в голове была ужасная путаница....
1 - Плз составить предложения из слов: 1. party, every week, have, we. 2. every...
3 - Найдите площадь с периметром 108 см и отношением стороны 3; 4; 5...
2 - 1)наиболее густонаселенные регионы африки 2)материк на территории которого...
3
ответ: №5 .