Решать, : ) sin^2 2x+ cos^2 3x=1+4sin x
Ответы
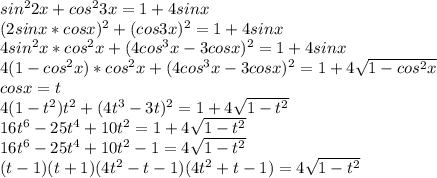 очевидно что он имеет только один корень равны
очевидно что он имеет только один корень равны 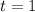 , потому что справа кв корень , он по ОДЗ
, потому что справа кв корень , он по ОДЗ 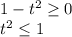 , слева очевидно что при
, слева очевидно что при 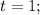 она обращается в 0 , откуда ответ
она обращается в 0 , откуда ответ 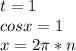
Другие вопросы по теме Алгебра
Популярные вопросы
- Вычислить пределы функции....
3 - Нужна с немецким языком. Фото прикреплено ниже...
2 - Проверяемое задание 4 (Блок Writing 2) Раздел 2. Работа в компании Задание Напишите...
2 - решить через свойства касательных и секущих...
3 - Складіть рівняння реакцій....
1 - Вычислите количество вещества (моль) в 98,0 граммах уксусной кислоты СН 3 СООН!...
2 - с сочинением на тему вид предмета для пятого класса...
1 - Вопросы и задания с рассказа ТАРАС БУЛЬБА...
3 - тип хімічного зв язку, тип кристалічної гратки, запах, температура плавлення,...
3 - Два студенти незалежно один від одного розв язують задачу. Ймовірності розв...
2