Ребята злелайде сколько сможете 4 делать не нужно

№1

1) х ∈ [-4; 1]

2) х ∈ (-∞; 0] ∪ [2; +∞)

3) х ∈ (-∞;+∞)

4) х ∈ [5; +∞)

5) х ∈ (-∞; -2] ∪ [3; +∞)

№2

1) х ∈ (-4.6; 1.3) ∪ (1.3; +∞)

2) х ∈ [-2.25; 1]

№3

1) х ∈ [0; 4]

2) х ∈ (-5; )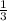

Объяснение:

№1 Спочатку вирішується як звичайне рівняння, потім знаходимо проміжок який нам потрібен і записуємо у відповідь.

1) x² + 3x - 4 < 0

(Всі рівняння я буду вирішувати за до дискримінанту)

D = b² - 4ac = 9 - 4 × 1 × (-4) = 9 + 16 = 25

x₁ =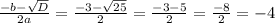

x₂ =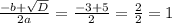

(У перший раз я розписав дискримінант повністю, надалі я так робити не буду)

Беремо будь-яке число у проміжку від -4 до 1 (наприклад 0) і підставляємо його у рівняння:

0² + 3 × 0 - 4 < 0

-4 < 0

Нерівність виконується для проміжку від -4 до 1. Отже х ∈ [-4; 1].

2) 4х² - 8х ≥ 0

Поділимо усе на 4 для спрощення:

х² - 2х ≥ 0

D = 4 - 4 * 1 * 0 = 4

x₁ =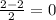

x₂ =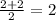

Беремо будь-яке число у проміжку від 0 до 2 (наприклад 1) і підставляємо його у рівняння:

1 - 2 ≥ 0

-1 ≥ 0

Нерівність не виконується, отже проміжок від 0 до 2 не підходить, отже:

х ∈ (-∞; 0] ∪ [2; +∞)

3) x² - 6x + 10 > 0

D = 36 - 4 * 1 * 10 = 36 - 40 = -4

Так як дискримінант менше нуля, то рівняння не має дійсних коренів. Візьмемо будь-яке число з проміжку (-∞;+∞), наприклад 0:

10 > 0

Нерівність виконується. Отже: х ∈ (-∞;+∞)

4) х² - 10х + 25 ≤ 0

D = 100 - 4 * 1 * 25 = 100 - 100 = 0

Оскільки дискримінант = 0, то рівняння має лише один корень:

х =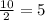

Візьмемо будь яке число з проміжку (-∞; 5), наприклад 0:

25 ≤ 0

Нерівність не виконується, отже проміжок (-∞; 5) не підходить, отже:

х ∈ [5; +∞)

5) (х + 2) * (х - 3) > 0

Щоб вираз дорівнював 0, достатньо щоб хоча б один з множників дорівнював 0:

х + 2 = 0          або          х - 3 = 0

х = - 2              або          х = 3

Візьмемо будь-яке число від -2 до 3 (наприклад 0):

(0 + 2) * (0 - 3) > 0

2 * (-3) > 0

-6 > 0

Нерівність не виконується, отже:

х ∈ (-∞; -2] ∪ [3; +∞)

№2

1) Щоб ділення дорівнювало 0, потрібно щоб чисельник дорівнював 0. Але для початку треба знайти область допустимих значень (знаменник не може дорівнювати 0 тому що на 0 ділити не можна):

ОБС:

х - 1.3 ≠ 0

х ≠ 1.3

Тепер можна вирішувати рівняння:

х + 4.6 > 0

х > -4.6

Отже: х ∈ (-4.6; 1.3) ∪ (1.3; +∞)

2) Найлегше відкрити скобки і перенести 9 у ліву частину при цьому змінити знак на протилежний:

4х² + 7х - 11 ≥ 0

D = 49 - 4 * 4 * (-11) = 49 + 176 = 225

x₁ =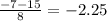

x₂ =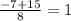

Будь-яке число від -2.25 до 1 (наприклад 0):

-11 ≥ 0

Нерівність виконується, отже проміжок нам підходить:

х ∈ [-2.25; 1]

№3 Область визначення це ті числа яких може набувати "х"

1) Число під коренем не може буди від'ємним, отже:

ОДС: 4х - х² ≥ 0

х × (4 - х) ≥ 0

х ≥ 0    або     4 ≥ х

х має бути більше (або дорівнювати) за 0, але менше (або дорівнювати) за 4.

Отже: х ∈ [0; 4]

2) Рівняння під коренем яке ще й при цьому знаходиться у знаменнику має бути строго більше за 0.

ОДС: 5 - 14х - 3х² > 0

Помножимо усе на -1 (не забувши при цьому змінити знак нерівності на протилежний):

3х² + 14х - 5 < 0

D = 196 - 4 * 3 * (-5) = 196 + 60 = 256

x₁ =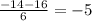

x₂ =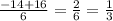

Візьмемо будь-яке число з цього проміжку (0):

- 5 < 0

Нерівність виконується, отже:

х ∈ (-5;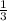 )