Разложение многочленов на множители группировки m-n+2p(m-n)
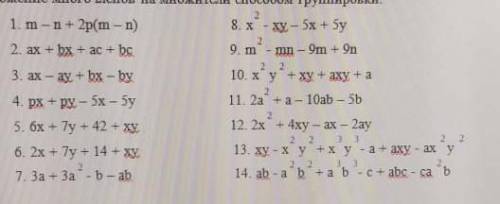
Другие вопросы по теме Алгебра
Популярные вопросы
- Подумайте, зачем нужны одежда и обувь....
3 - Как следует заботиться о своей одежде и обуви?...
3 - Какие правила гигиены надо соблюдать при уходе за зубами, ногтями,...
2 - Объясните, почему в народе говорят: «Мойся белее — будешь здоровее»....
2 - Вспомните, что нужно человеку для жизни. Почему правильное питание...
2 - Рассмотрите рисунки. Обсудите, какие из этих продуктов питания полезны...
3 - Рассмотрите рисунки. Кто из детей соблюдает, а кто нарушает правила...
3 - Подумайте, сколько раз в день надо есть, чтобы быть сытым и здоровым....
1 - Почему правильное питание важно для человека?...
1 - Какие правила режима питания нужно соблюдать?...
3
1. Шаг: Выделяем общий множитель:
В данном случае, общим множителем является (m - n), поэтому мы можем записать заданный многочлен так:
(m - n) + 2p(m - n)
2. Шаг: Группируем слагаемые:
Мы можем группировать слагаемые, помещая их в скобки:
(m - n)(1 + 2p)
Теперь мы получили разложение данного многочлена на множители группировки.
Давай проверим правильность нашего ответа, раскрыв данное выражение:
(m - n)(1 + 2p) = m(1 + 2p) - n(1 + 2p)
Раскрываем скобки:
m + 2pm - n - 2pn = m - n + 2pm - 2pn
После сбора подобных слагаемых, мы получаем исходное выражение m - n + 2p(m - n), что означает, что наше разложение верно.
Важно отметить, что в данной задаче мы использовали метод группировки, который подразумевает группировку слагаемых с общим множителем и их последующее вынесение за скобки. Чтобы правильно применить этот метод, необходимо уметь определить общий множитель в заданном выражении.