Расположите в порядке возрастания значения: а) синусов;
в) тангенсов
г) котангенсов углов
б) косинусов;
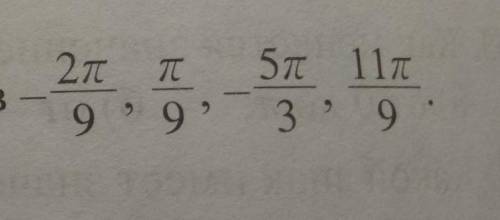
Другие вопросы по теме Алгебра
Популярные вопросы
- кто читал приключение Тома Сойера Итак вопрос:Какое наказание потерпел том...
3 - Вот не спамьте я же ведь всё равно пасипо...
1 - Що нового ви дізналися про жанр прелюдії? Пояснить на прикладі творчості...
1 - решите задачу с Дано и Решением. не только ответ. и еще у мен есть еще вопрос,...
3 - СРЧНООО Венн диаграммасында көмекші ақпараттарды пайдалана отырып, Англия...
3 - 7. Состав изумрудно-зеленого минерала малахита выражается химической формулой...
3 - Choose the correct item, 1 Uncle Tom s Cabin is set on/in the USA. 2 I was...
2 - Составьте программу для нахождения температуры Tf в градусах Фаренгейта,...
2 - Read the text that follows. Use the words in the box to form words that fit...
2 - 1. (√ 50 - √18) × √2 25√X × 4√Y 2. при X=4 Y=8 √XY 3. 0,5√0,04 - 7/6√36 (2√3)²...
2
Сначала давайте разберемся с определениями и свойствами каждой из функций:
1) Синус (sin): В геометрии, синус угла равен отношению противолежащего катета к гипотенузе прямоугольного треугольника. Он обозначается как sin(угол). Значения синуса изменяются в диапазоне от -1 до 1.
2) Косинус (cos): Косинус угла равен отношению прилежащего катета к гипотенузе прямоугольного треугольника. Он обозначается как cos(угол). Значения косинуса также изменяются в диапазоне от -1 до 1.
3) Тангенс (tan): Тангенс угла определяется как отношение синуса угла к косинусу угла. Он обозначается как tan(угол). Значения тангенса могут быть отрицательными, положительными или бесконечными.
4) Котангенс (cot): Котангенс угла определяется как обратное значение тангенса угла. Он обозначается как cot(угол).
Теперь, давайте проанализируем данный график, чтобы определить порядок возрастания каждой из функций.
Сначала посмотрим на график синуса (a). Мы видим, что синус углов изображен на графике с помощью черных точек. На оси ординат мы имеем значения синуса, а на оси абсцисс углы в градусах. Заметим, что значения синуса углов на графике постепенно возрастают с увеличением угла. Таким образом, значения синусов возрастают по мере увеличения углов.
Затем рассмотрим график косинуса (б). Косинус углов изображен на графике с помощью красных точек. Опять же, значения косинуса углов находятся на оси ординат, а значения углов находятся на оси абсцисс. На графике видно, что значения косинусов углов убывают с увеличением угла. То есть, с увеличением угла, значения косинусов уменьшаются.
Далее обратимся к графику тангенсов (в). Тангенсы углов представлены на графике с помощью синего цвета. Как видно, значения тангенсов возрастают с увеличением угла.
Наконец, график котангенсов (г) представлен на графике зелеными точками. Мы видим, что значения котангенсов также возрастают по мере увеличения угла.
Таким образом, порядок возрастания функций будет следующим:
а) Синусы
б) Косинусы
в) Тангенсы
г) Котангенсы