про квадратный трехчлен f(x) известно, что уравнение f(x) =5x-20 имеет единственный корень и уравнение f(x) =2x-8 имеет единственный корень. Найдите наибольшее значение, которое может принимать дискриминант трехчлена f(x) ​

Пусть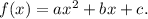 Данные уравнения могут быть записаны в виде

По условию эти уравнения имеют единственные корни, что бывает тогда и только тогда, когда их дискриминанты равны нулю, то есть

Домножим первое выражение на 2, а второе на 5, после чего возьмем их разность:

откуда дискриминант исходного квадратного трехчлена равен

Таким образом, дискриминант равен 10, а значит наибольшее значение, которое он может принимать, также равен 10.

ответ: 10