При каком значении "а" , один из корней уравнения x²-3ax+5=0 равен 2?
Другие вопросы по теме Алгебра
Популярные вопросы
- Какая масса нитрата серебра вступит в реаецию с хлоридом натрия...
2 - Преспокойно , серебряный-морфемный разбор...
2 - Науково технічні відкриття кінця XIX початку XX сторіччя і їх вплив...
2 - 3. Почему XIX век в Европе оказался таким богатым на разного рода...
2 - Хронология Сопоставьте древние цивилизации с описанием некоторых...
3 - завтра сдавать! Лабраторная работа номер 7, 7 класс учебник сухова...
1 - C→CO2→H2CO3→MgCO3→CO2решите цепочку...
2 - Сіль, ступінь, здоров я, заєць, пояс, рельєф, яблуня, жолудь, юрист,...
3 - Выполните по образцу: Торопимся (гл. 1л., мн.ч.) в бассейн.(односост.,...
3 - |x + 5| + 2=2 Знайти модуль...
2
ответ: 1.5.
Объяснение:
x²-3ax+5=0;
x1+x2=3a;
x1*x2=5;
пусть х1=2.
2+х2=3а;
2*х2=5;
x2=2.5;
2+2.5=3a;
3a=4.5;
a=1.5.
x^2-3*1.5x+5=0;
x^2-4.5x+5=0;
по т. Виета
x1+x2=4.5;
x1*x2=5
x1=2; x2=2.5.
Решение.
.
Если один из корней равен 2 , то подставив в уравнение вместо х
число 2, получим верное равенство:
.
Если один из корней равен 2 , то второй корень по теореме Виета можно найти из соотношения
И из соотношения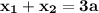 получим
получим