при каком наименьшем целом значении параметра а неравенство
справедливо для любого х>3?
Другие вопросы по теме Алгебра
Популярные вопросы
- Турбота про ближнього ось шо мусило стати морю справой...
3 - Развернутый ответ на проблемный вопрос Какие особенности характера Владимира...
2 - Общая характеристика китая история 7 класс 3-4 предложение...
3 - Составить 4 отрицательных предложения (два с отрицанием nicht, два с отрицанием...
2 - Решите задание на картинках...
2 - Знайдіть значення виразу(завдання в прикріпленому файлі, задание в прикреплённом...
3 - Твир-опыс картины Оля Билокур...
2 - каковы главные идеи и принципы реализма? перечислите известнейших писателей...
3 - Які труднощі доводилось долати мешканцям стародавньої Індії?...
1 - Сульфид железа (1) массой 140,8 г обработали хлороводородной кислотой. Выделившийся...
2
Рассмотрим сначала особую точку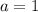 --- там парабола вырождается в прямую. Тогда
--- там парабола вырождается в прямую. Тогда
Значит, все дальнейшие рассуждения проводим при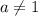 .
.
Найдём корни функции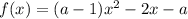 :
:
где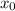 --- вершина параболы и по совместительству точка экстремума функции
--- вершина параболы и по совместительству точка экстремума функции 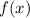 .
.
Значение функции в этой точке равно
Из исследования знаков производной/функции легко установить, что при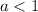 величина
величина 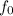 --- максимум (это, впрочем, понятно и из вида функции
--- максимум (это, впрочем, понятно и из вида функции 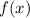 ), больший нуля. Причём в этом случае
), больший нуля. Причём в этом случае  , т.е. понятно, что в области
, т.е. понятно, что в области 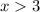 функция будет падать от какого-то максимального положительного (это в лучшем случае, а может уже и от отрицательного) значения. В любом случае, рано или поздно значение функции станет меньше нуля.
функция будет падать от какого-то максимального положительного (это в лучшем случае, а может уже и от отрицательного) значения. В любом случае, рано или поздно значение функции станет меньше нуля.
Таким образом, рассматриваем значения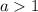 .
.
Ну, раз просят наименьшее целое значение параметра, то не будем далеко ходить и рассмотрим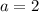 .
.
Корни и точка экстремума:
Теперь уже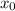 - минимум функции, а (после аналогичного анализа)
- минимум функции, а (после аналогичного анализа) 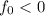 .
.
Если нам повезёт, то правый (который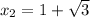 ) корень будет лежать левее точки
) корень будет лежать левее точки 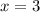 , а это будет означать, что к тому времени как функция подойдёт к
, а это будет означать, что к тому времени как функция подойдёт к 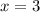 , она уже будет положительна (ведь правее экстремума
, она уже будет положительна (ведь правее экстремума 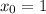 парабола рогами вверх будет идти только вверх). Исследуем:
парабола рогами вверх будет идти только вверх). Исследуем:
Победа.
ответ.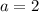 .
.