При каких значениях 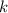
прямая
имеет единственную общую точку с графиком
функции
?
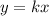
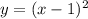
Другие вопросы по теме Алгебра
Популярные вопросы
- Теңсіздікті шеш 3(2х-3)+8 8х+3...
3 - 5 Заданне. Надпиши число и время глаголов В марте прилетел к нам грач...
1 - На рисунку точка О центр кола, хорди АВ і СД рівні.Укажіть усі пари...
3 - N 387. Выполните действия решите в скобках если решите правильно и в...
1 - ХЕЛП Космонавт вступил на недавно открытую планету за пределами Солнечной...
2 - Каштан Плоды каштана защищает коричневая скорлупочка. У неё острые колючки....
3 - Белгісіздік мағынаны білдіретін сөздермен сөйлем құрастыр.(4 ұпай) Кейбір,...
2 - 1. Чому ще нікому не вдалось надути звичайну повітряну кульку, щоб вона...
1 - Сочинение рассуждение Какая игрушка лучше Купленная или сделанная сврими...
1 - Основатель монгольской империи Чингизхан родился в каком году а) 1206...
3
Из условия следует, что прямая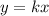 должна быть касательной к графику функции
должна быть касательной к графику функции 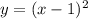 .
.
В точках касания равны значения функции и их производные, т.е. имеет место система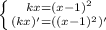
Подставим k из второго уравнения в первое:
Из равенства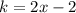 получаем, что
получаем, что 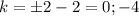
ОТВЕТ: k = -4, k = 0.